A solid sphere with a velocity (of centre of mass) $v$ and angular velocity $ω$ is gently placed on a rough horizontal surface. The frictional force on the sphere :

A

must be forward (in direction of $v$ )

B

must be backward (opposite to $v$ )

C

cannot be zero

D

none of the above

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Case I
(i) If $R ω > v$ than point of contact slides backward and friction direction.

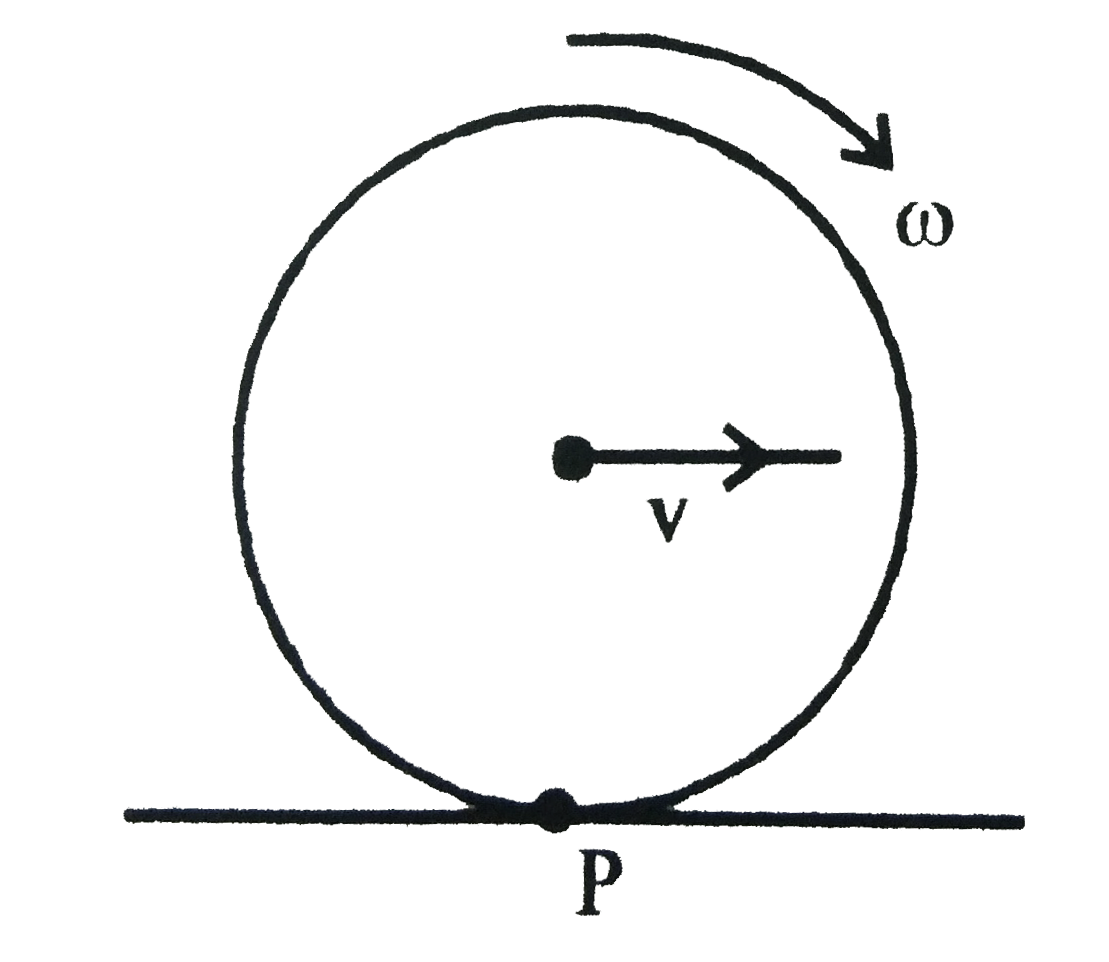
$v_{P} = v - R ω$
(ii) If $v > R ω$ than point contact slides forward and friction will act in backward direction
$v_{P} = v - R ω$
(iii) If $v = R ω, f = 0, v_{P} = 0$
Case II
so friction willm act in backward direction.
.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

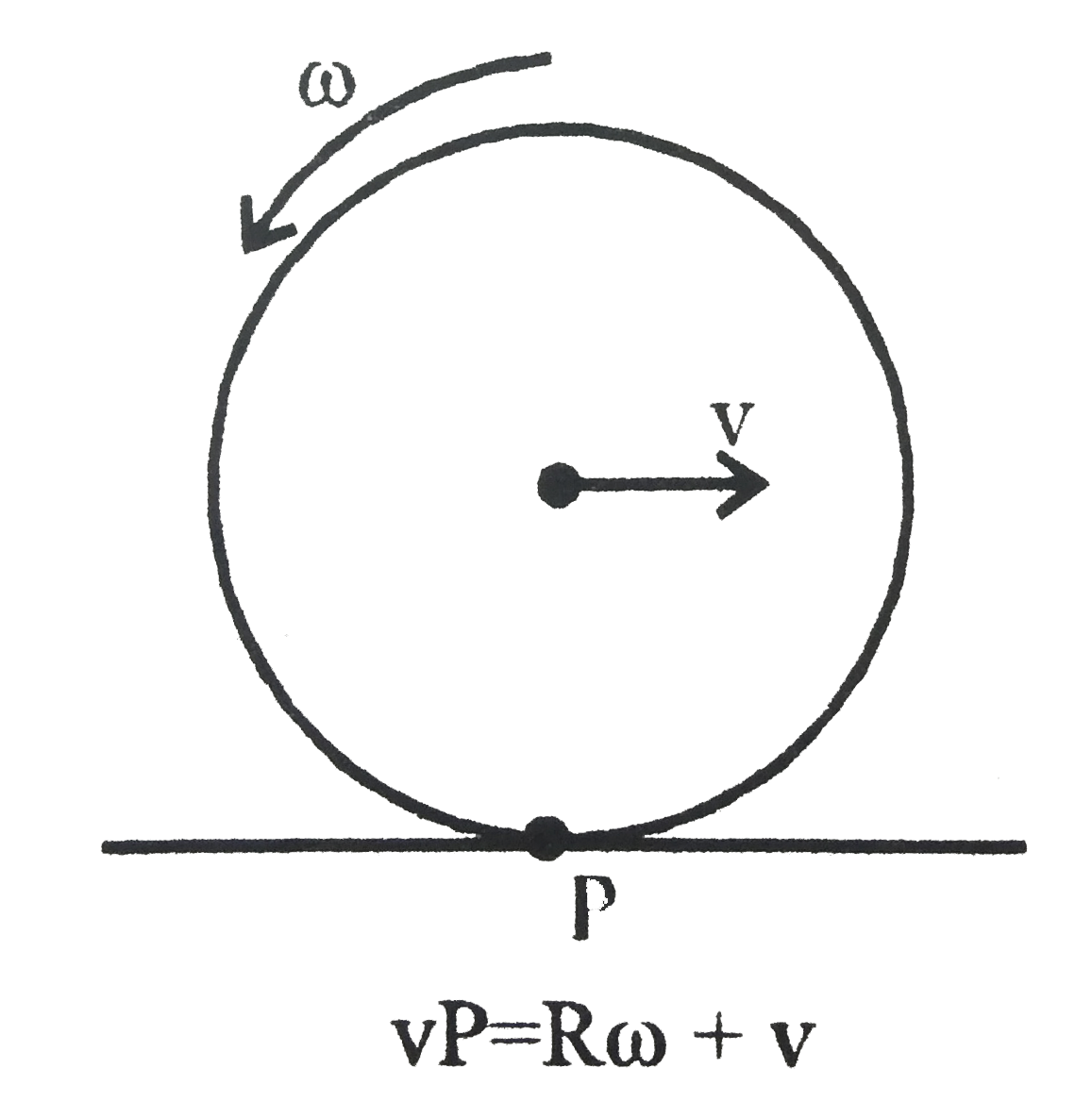Similar Questions

Knowledge Check

Question 1 - Select One
A ring of radius $R$ is first rotated with an angular velocity $ω$ and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is $μ$ . Time after which its angular speed is reduced to half is
A $\frac{ω_{0} μ R}{2 g}$
B $\frac{ω_{0} g}{2 μ R}$
C $\frac{2 ω_{0} R}{μ g}$
D $\frac{ω_{0} R}{2 μ g}$
Question 2 - Select One
A hoop of radius r and mass m rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
A $\frac{r ω_{0}}{4}$
B $\frac{r ω_{0}}{3}$
C $\frac{r ω_{0}}{2}$
D $r ω_{0}$
Question 3 - Select One
A hoop of radius $r$ mass $m$ rotating with an angular velocity $ω_{0}$ is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
A $\frac{r ω_{0}}{2}$
B $r ω_{0}$
C $\frac{r ω_{0}}{4}$
D $\frac{r ω_{0}}{3}$

Recommended Questions

Home
Ask Doubt
Profile