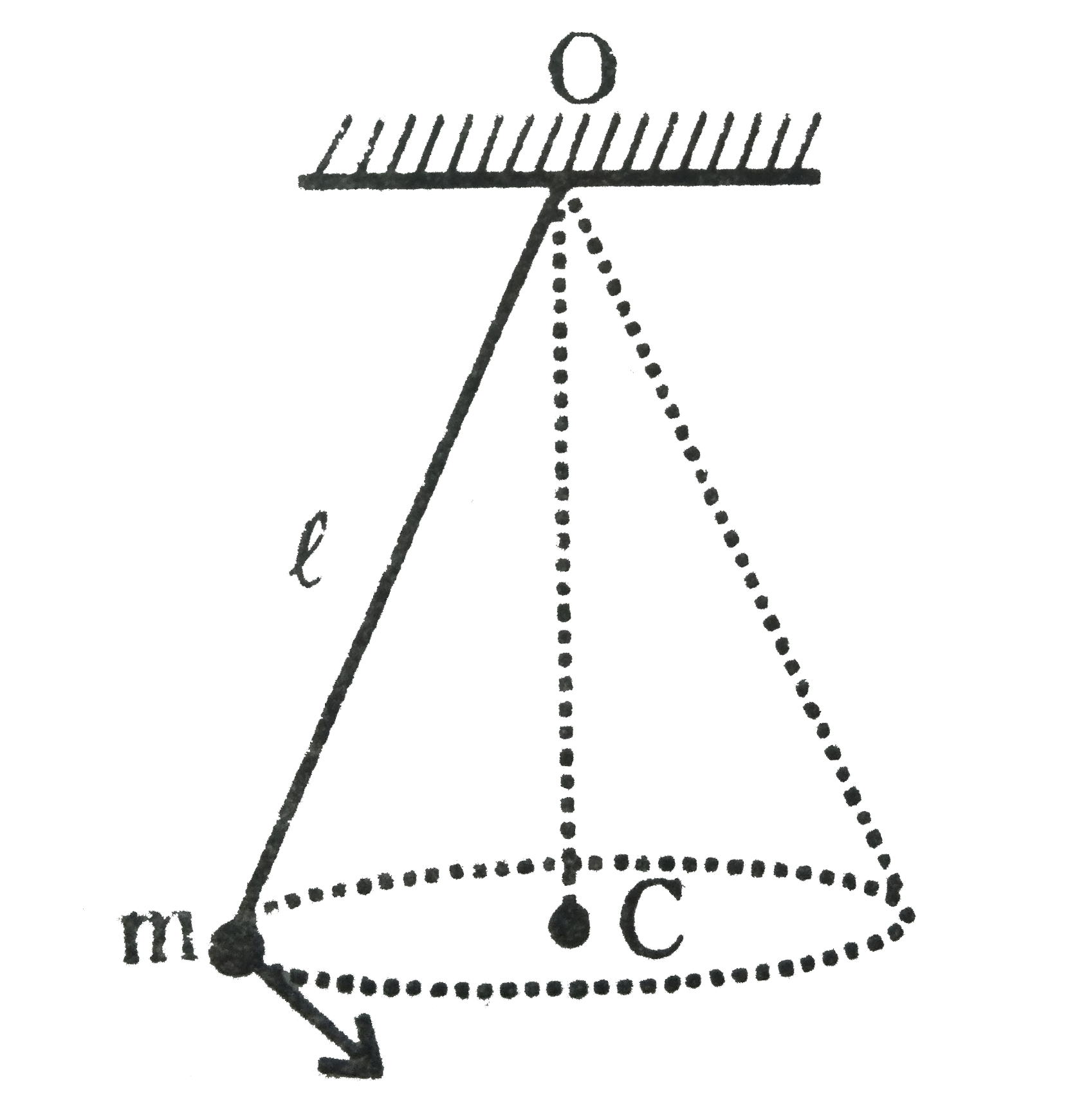
A small ball of mass $m$ suspended from the celling at a point $O$ by a thread of length $l$ moves along a horizontal circle with a constant angular velocity $ω$ .
.

linear momentum of system (ball + rod) is conserved

angular momentum about C is conserved

kinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collision

linear momentum of ball is conserved

Text Solution

Verified by Experts

The correct Answer is:B, C, D

Updated on:21/07/2023

A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
A $\frac{r g}{\sqrt{L^{2} - r^{2}}}$
B $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
C $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
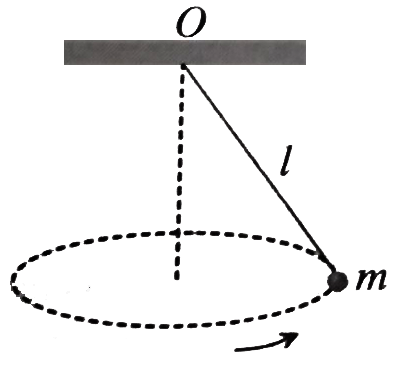
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass are
A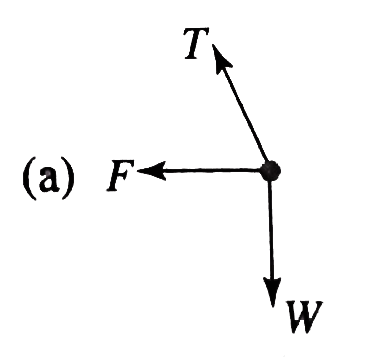
B
C
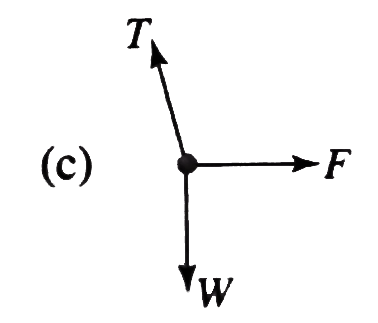D
Two masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity $ω$ . If the tensions in the threads are the same during motion, the distance of M from the axis is
A $\frac{M l}{M + m}$
B $\frac{m l}{M + m}$
C $\frac{M + m}{M} l$
D $\frac{M + m}{m} l$