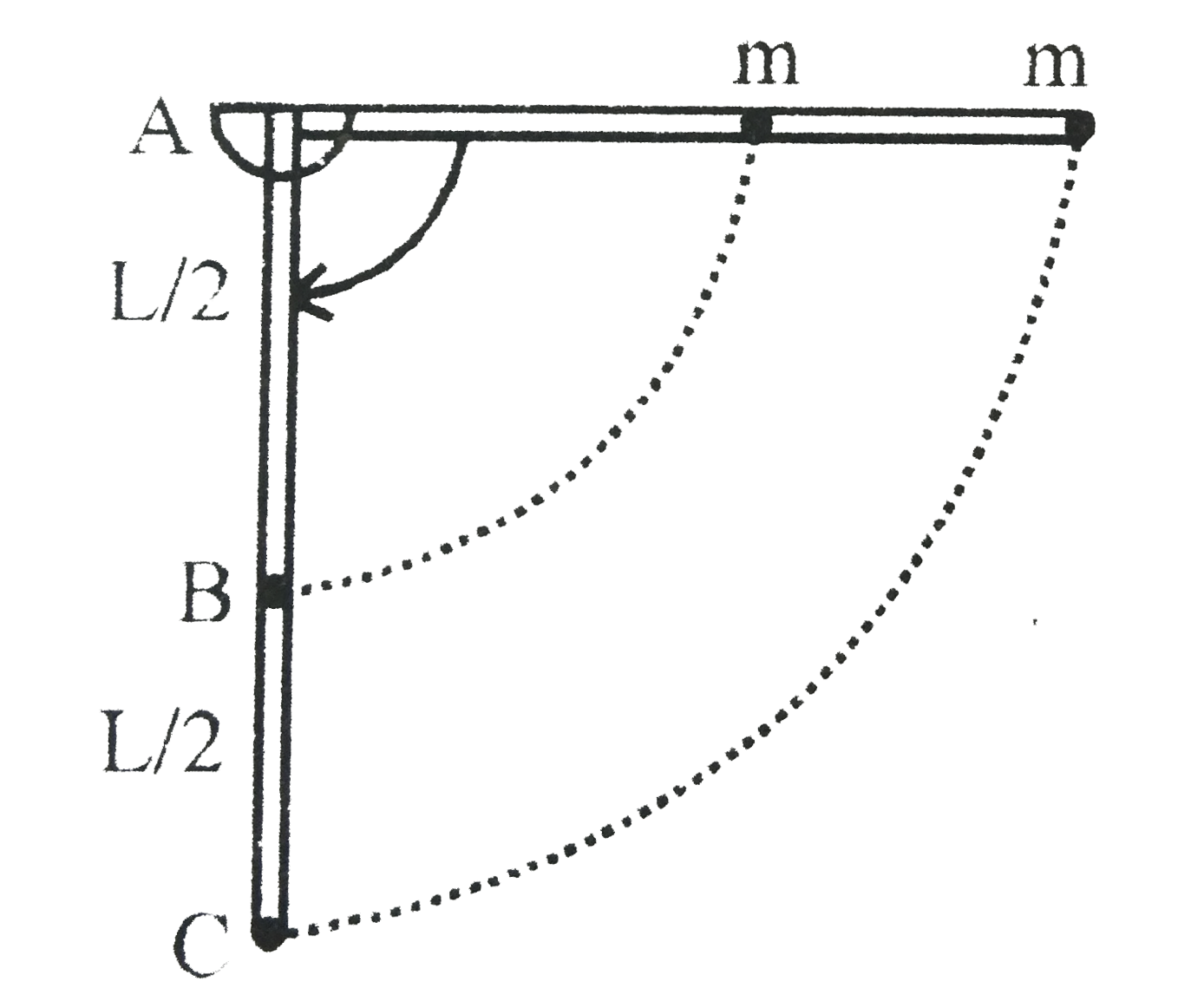
Two masses each of m are attached at mid point B and end point C of massless rod AC which is hinged at A. It is released from horizontal position as shown. Find the force at hinge A when rod becomes vertical.
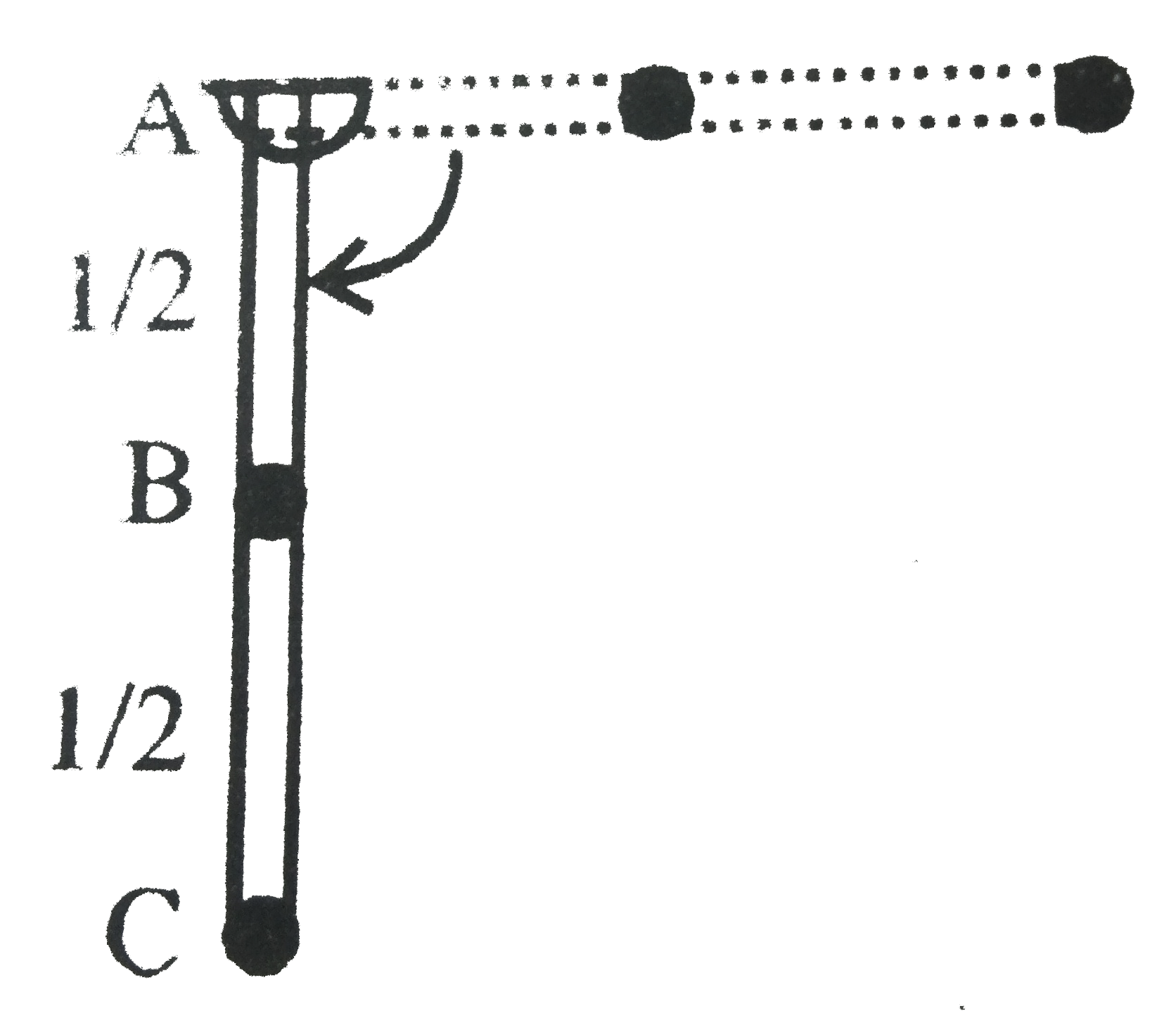 .
.
The correct Answer is:28mg5
The centre of mass particles B and C from A.
x=m×L2+mL2m
x=3L4
From Work Energy Theorem
WDgravity=ΔKE
2mg(3L4)=12Iω2
2mgL2=12(mL24+mL2)ω2
3mgL=(5mL24)ω2
ω2=12g5L....(1)
The force at hinge A provides necessary centripental force
T=2mh=(2m)ω2(3L4)
T=3mg+2m×12g5L×3L4⇒T=28mg5.
Similar Questions
A rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View Solution
Knowledge Check
One end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mgA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
 ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionIn the figure given in the text if mass of the rod is m then find hinge force.
(a). Just after the rod is released from the horizontal position.
(b). When rod becomes vertical
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionA simple pendulum A and a homogeneous rod B hinged at its enda are released from horizontal position as shown in figure.

View SolutionTwo blocks each of the mass m are attached to the ends of a massless rod which pivots as shown in figure. Initially the rod is held in the horizontal position and then released. Calculate the initial angular acceleration.

View Solution
