A uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find
(A) the angular velocity of the disc.
(B) the impulse on the particle due to disc
( C) the impulse on the disc due to hinge.

Text Solution
Verified by Experts

The correct Answer is:(a) ω/3,
(b) √373mωR
( c) √373mωR.

(a) From conservation of angular momentum
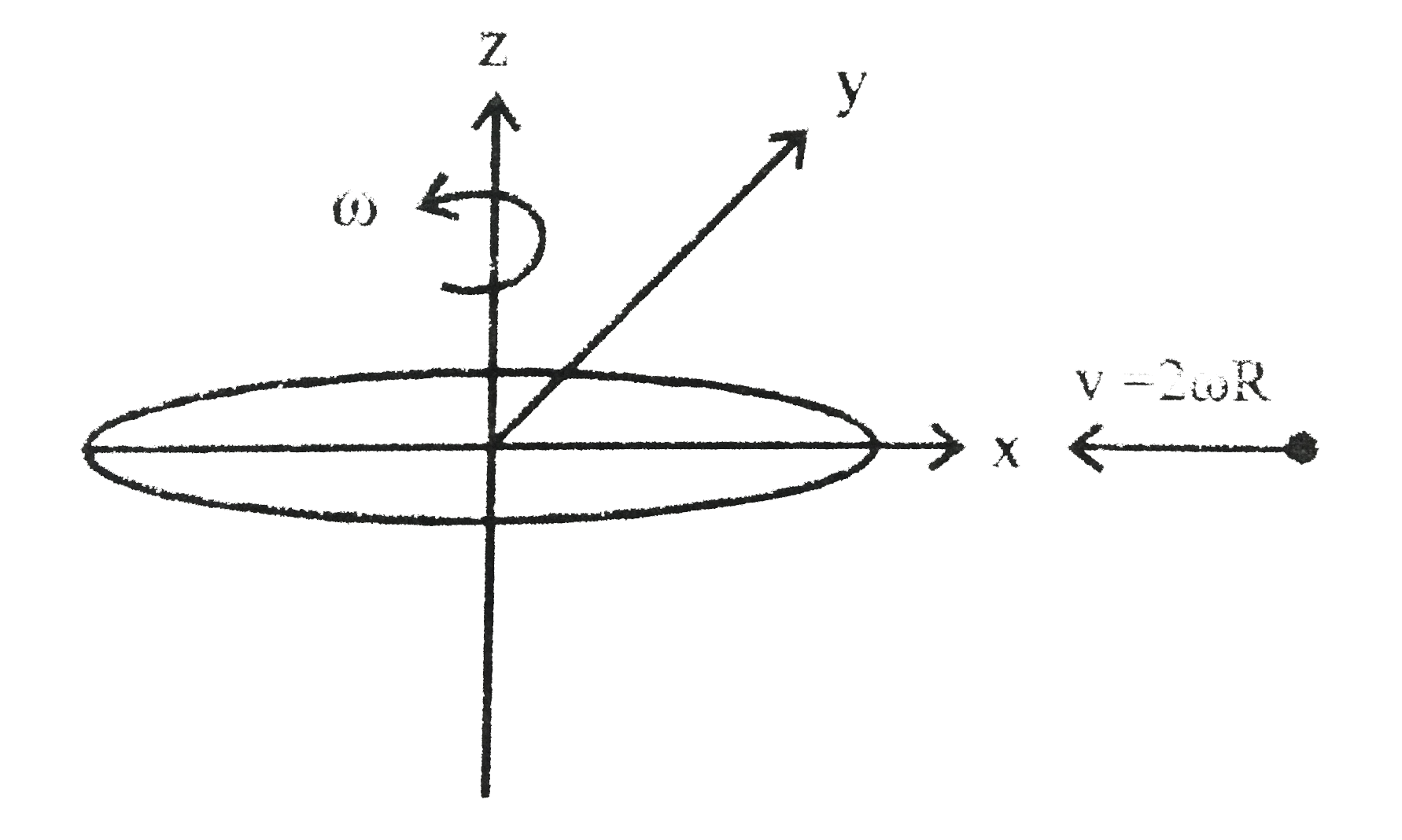
ocr_image
:. I1ω1=I2ω2
(12mR2)ω=(12mR2+mR2)ωf
12mR2ω=(32mR2)ωf
ωf=ω3
(b) Impulse = change in linear momentum
→J=mvfˆj−m(2ωR)(−ˆi)
→J=m(Rω3)ˆj+2mωRˆi
∣∣→J∣∣=√(mRω3)2+2mωR2
∣∣→J∣∣=mRω√19+4⇒∣∣→J∣∣=√373mRω
( c) Impulse on disc is equal and opposite to impulse on particle due to disc.
:. J=√373mRω.

Doubtnut Promotions Banner
|
Class 11PHYSICSRIGID BODY DYNAMICS

Similar Questions

Knowledge Check

  • A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
    The angular velocity of the disc after the particle sticks to it is

    Aω5
    Bω3
    Cω2
    Dω4

  • A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is

    A√173mωR
    B√353mωR
    C√373mωR
    D√293mωR

  • A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be

    A(M−2m)ω(M−m)
    B(M+2m)ω(M+m)
    C(M−2m)ω(M+m)
    D(M+2m)ω(M−m)