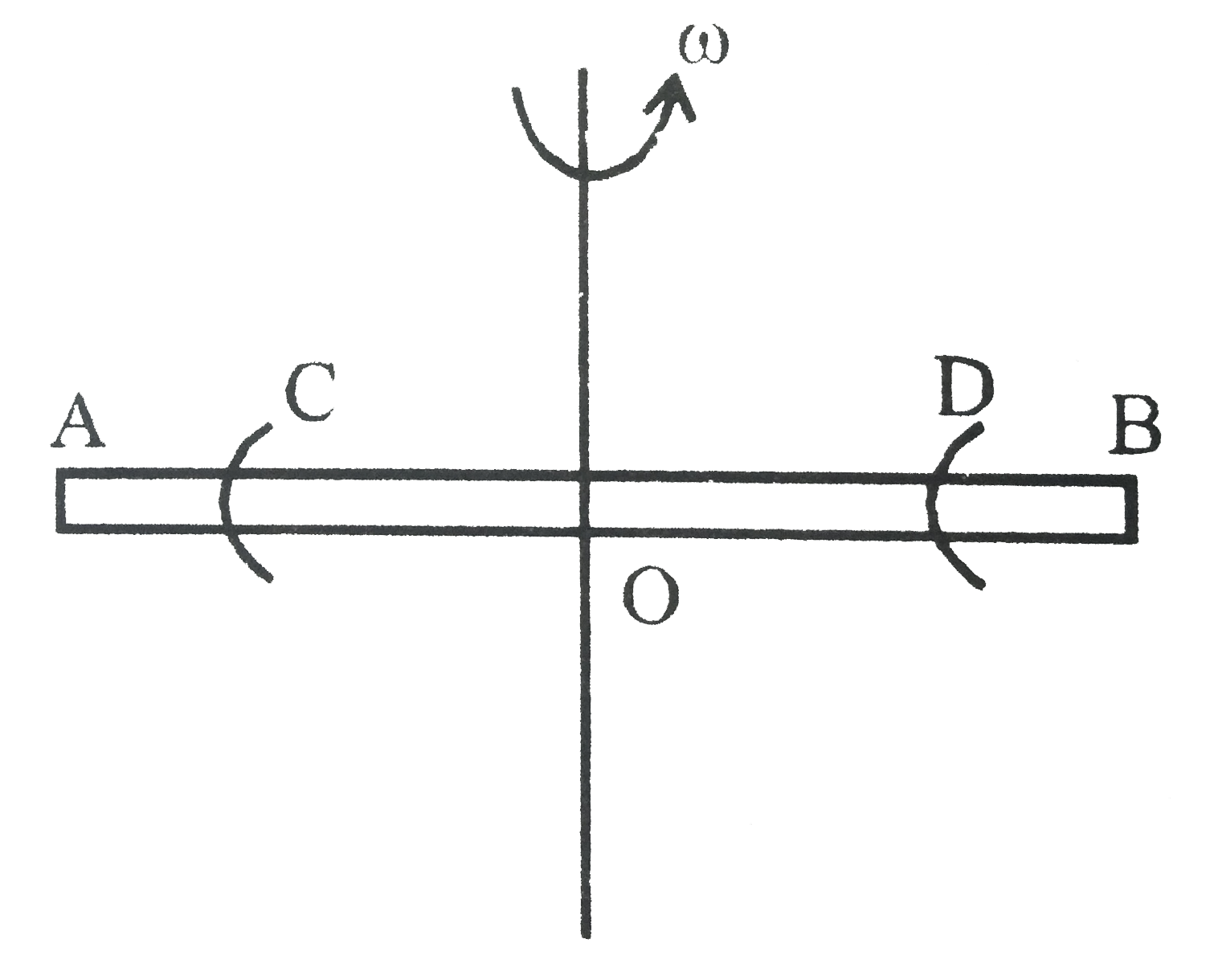
A rigid horizontal smooth rod AB of mass 0.75kg and length 40cm can roate freely about a fixed vertical axis through its mid point O. Two rings each of mass 1kg are initially at rest at a distance of 10cm from O on either side of the rod. The rod is set in rotatiob with an angular velocity of 30 radians per second. Find the velocity of each ring along the length of the rod in m/s when they reach the ends of the rod.
 .
.
The correct Answer is:3
From conservation of linear momentum
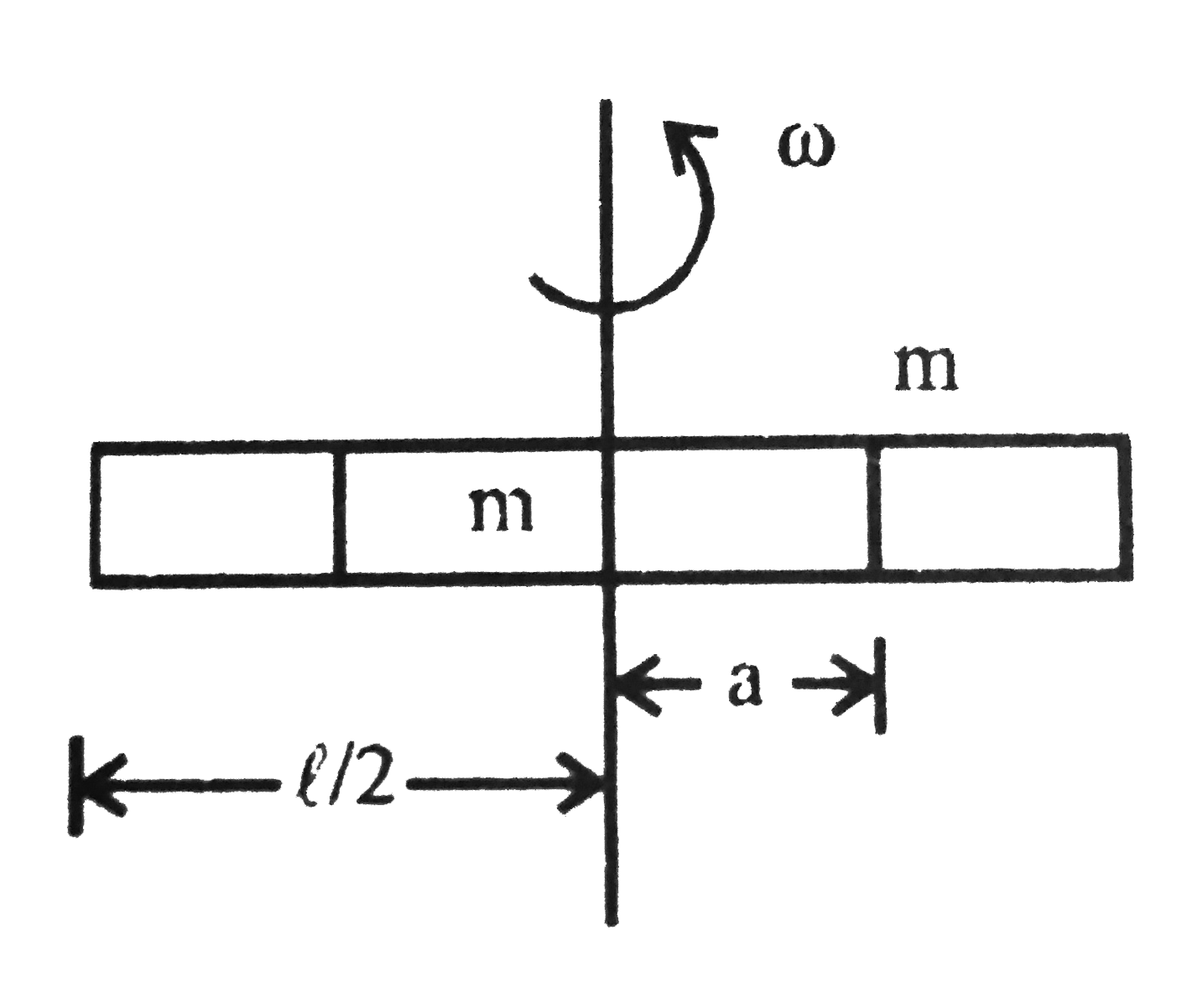
I1ω1=I2ω2
(ml212+2ma2)ω1=[(ml212+2m(l2)2)]ω2
ω2=10rad/sec
form conservation of energy
12I1ω21=12I2ω22+2×12mv2
v=3m/s.
Similar Questions
A horizontally oriented uniform rod AB of mass m=1.40kg and length l0=100cm rotates freely about a stationary vertical axis OO′ passing through its end A. The point A is located at the middle of the axis OO′ whose length is equal to l=55cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO′ is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
View SolutionA uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity V0 and sticks to it. The angular velocity of the combination immediately after the collision is:
View Solution
Knowledge Check
A rigid horizontal smooth rod AB of mass 0.75 kg and length 40 cm can rotate freely about a fixed vertical axis through its midpoint O. Two rings each of mass 1 kg initially at rest are placed at a distance of 10 cm from O on either side of the rod. The rod is set in rotation with an angular velocity of 30 radian per sec and when the rings reach the ends of the rod, the angular velocity in rad/sec is
A5B10C15D20A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 Aω0BMω0M+12mCMω0M+2mDMω0M+6m
Aω0BMω0M+12mCMω0M+2mDMω0M+6mA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity ω fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90∘
View Solution
