A particle of mass 4kg moves between two points A and B on a smooth horizontal surface under the aciton of two forces such that when it is at a point P, the forces are 2→PAN and 2→PBN. If the particle is released from rest at A, find the time it takes to travel a quarter of the way A to B.
The correct Answer is:π3s
Figure
Similar Questions
A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B. particle released from rest from mid point of AB.
Find the minimum distance of the particle from B during the motion.
View SolutionA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find its time period when released from rest from mid-point of line AB.
View Solution
Knowledge Check
A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find its time period when released from rest from mid-point of line AB.AT=2π√3agBT=2π√a2gCT=2π√agDT=2π√a3gA particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.A√2ga3B√2ga6C√2ga5D√ga3A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find the minimum distance of the particle from B during the motion.Aa6Ba4Ca3Da8
A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
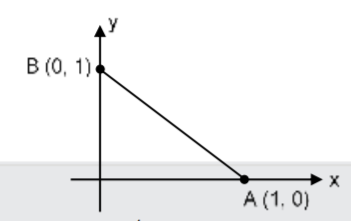
View SolutionIn the shown figure, mass m rests on smooth horizontal surface, connected with an ideal spring. If mass is displaced to the point A and released from rest, it reaches the point O in time t0.
Now the block is displaced to the point B and released from rest. How much time it will take in travelling from point A to point O.
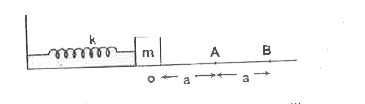
View SolutionIn the shown figure, mass m rests on smooth horizontal surface, connected with an ideal spring. If mass is displaced to the point A and released from rest, it reaches the point O in time t0.
Now the block is displaced to the point B and released from rest. How much time it will take in travelling from point A to point O.

View SolutionA particle moves in the x-y plane under the action of a force →F such that the value of its linear momentum →P at any time t is Px=2 cost and py=2sint. What is the angle θ between →F and P at a given time t?
View Solution
