An object is projected vertically upward from the surface of the earth at which above and below the surface acceleration due to gravity is the same.
The correct Answer is:h=√5−12R
Let at height or depth h from the surface of earth acceleration due to gravity is same.
gd=gh
g(1−hR)=gR2(R+h)2⇒(R−h)R=R2(R+h)2
(R−h)(R+h)2=R3
(R−h)(R2+h2+2hR)=R3
R3+Rh2+2hR2−hR2−h3−2h2R=R3
h3+h2R−hR2=0
h2+hR−R2=0
h=−R±√R2+4R22⇒h=(√5−1)R2
Similar Questions
Knowledge Check
- Question 1 - Select One
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A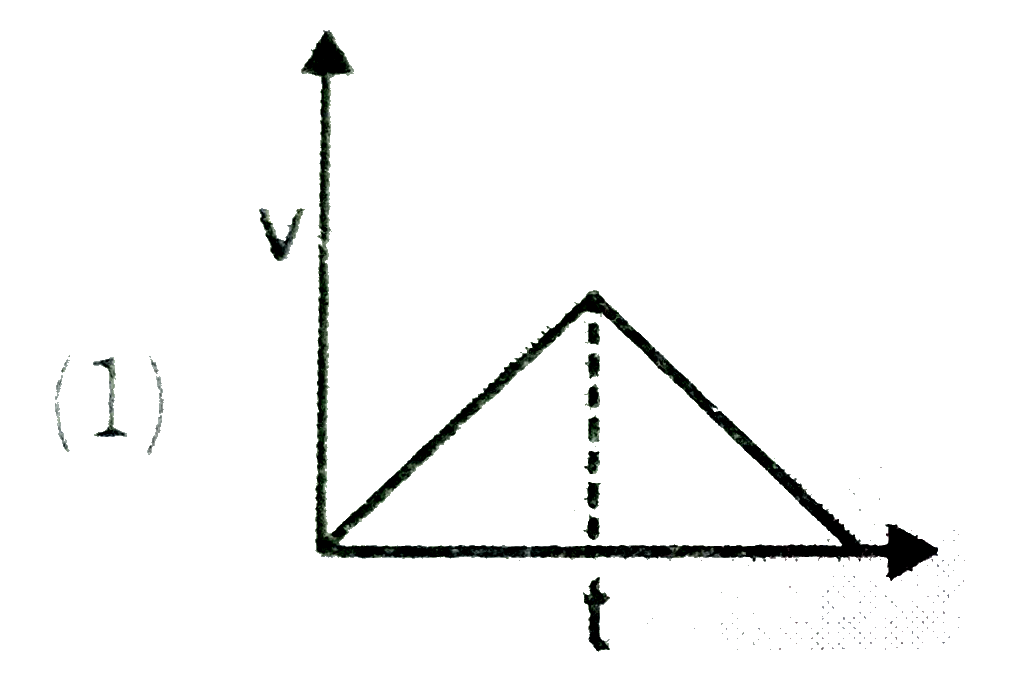 B
B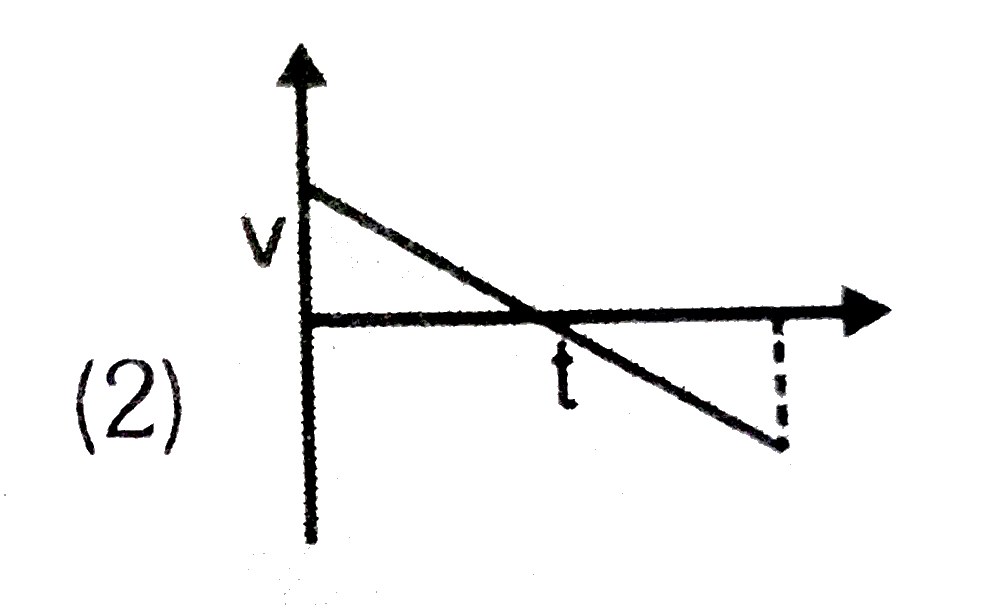 C
C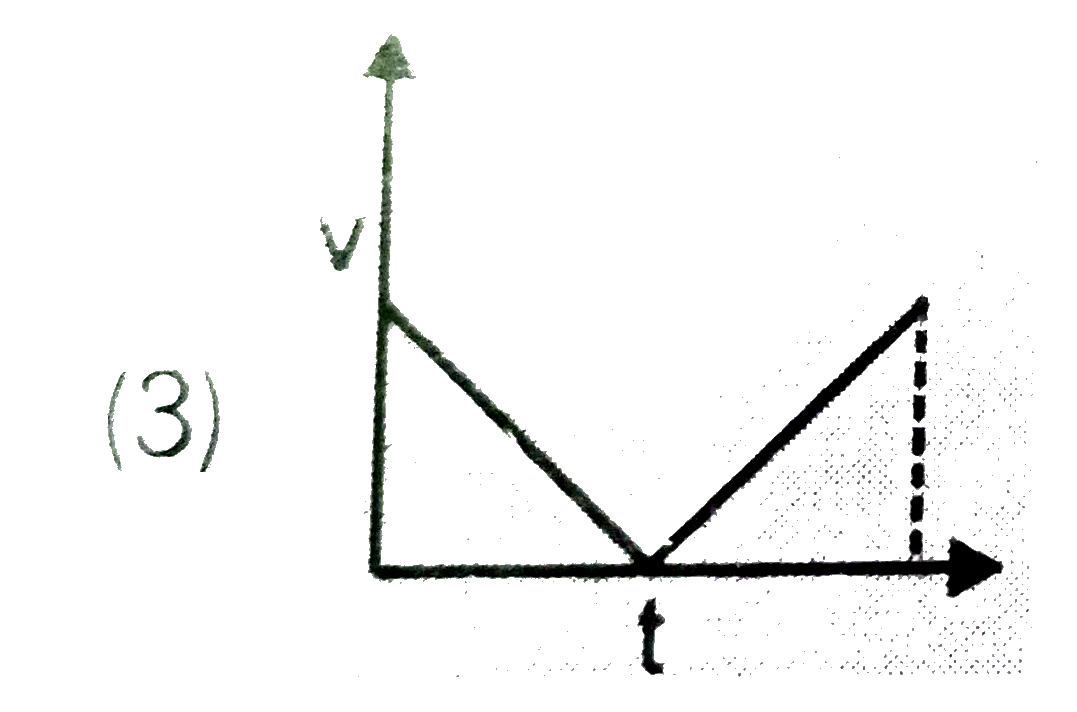 D
D
- Question 2 - Select One
An objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
A√2veB2√2veC2veDve√2 - Question 3 - Select One
At a height equal to earth's radius, above the earth's surface, the acceleration due to gravity is
AgBg2Cg4Dg8
" The distance from the surface of the earth at which the acceleration due to gravity is the same below and above the surface of the earth."
View SolutionA body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionAs we go above the earth's surface , the value of acceleration due to gravity increases.
View SolutionThe value of acceleration due to gravity at the surface of earth
View SolutionA particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
View Solution


