A remote sensing satellite is revolving in an orbit of radius $x$ above the equator of earth. Find the area on earth surface in which satellite can not send message.

Text Solution

Verified by Experts

The correct Answer is: $(1 - \frac{\sqrt{x^{2} - R^{2}}}{x}) 4 π R^{2}$

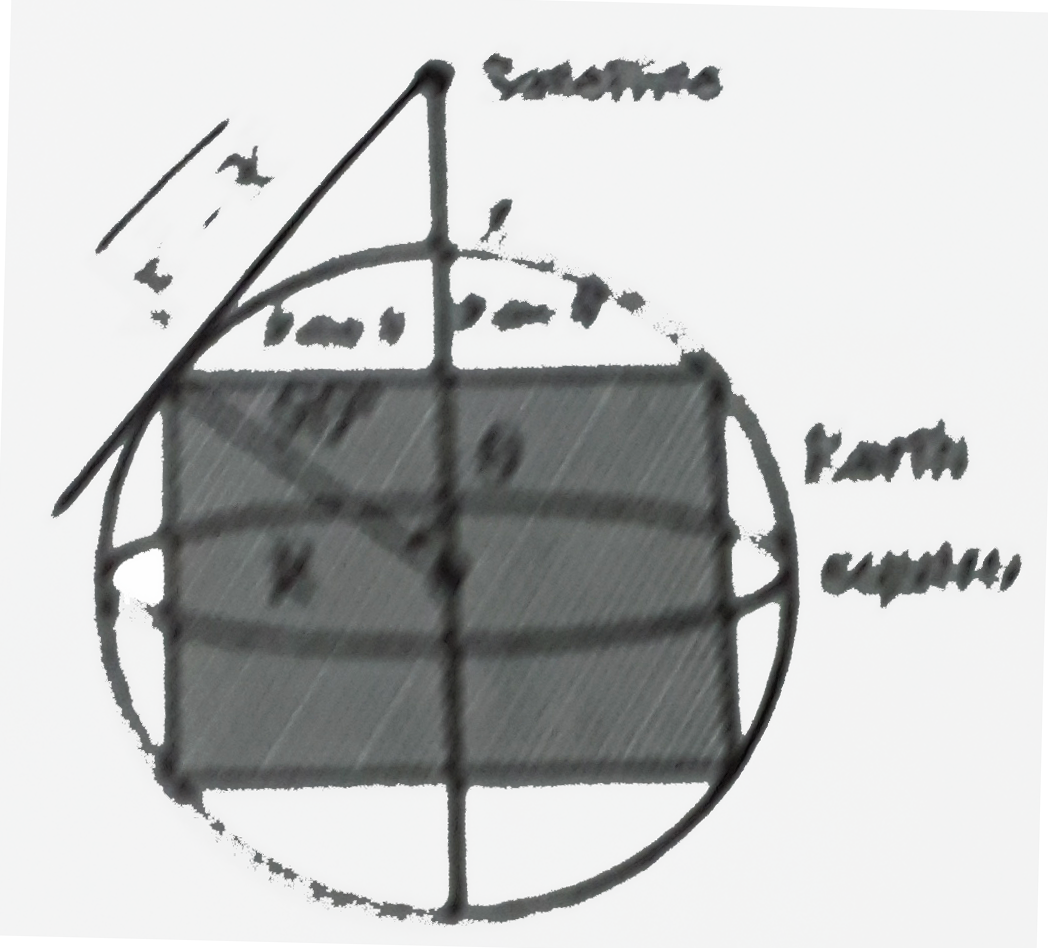
Area of strip = $2 R sin θ \times 2 π R$
$= 4 π R^{2} sin θ$
Area of strip $= 4 π R^{2} \frac{\sqrt{x^{2} - R^{2}}}{x}$
Area not covered $= 4 π R^{2} - 4 π R^{2} \frac{\sqrt{x^{2} - R^{2}}}{x}$
$= (1 - \frac{\sqrt{x^{2} - R^{2}}}{x}) 4 π R^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Similar Questions

Knowledge Check

Question 1 - Select One
Remote sensing satellites move in an orbit that is at an average height of about $500 k m$ from the surface of the earth. the camera onboard one such satellite has a screen of area $A$ on which the images captured by it are formed. If the focal length of the camera lens is $50 c m$ , then the terrestrial area that can be observed from the satellite is close to
A $2 \times 10^{3} A$
B $10^{6} A$
C $10^{12} A$
D $4 \times 10^{12} A$
Question 2 - Select One
The potential energy of a satellite of mass m revolving at height $R$ above the surface of the earth where $R =$ radius of earth is
A $- m g R$
B $- \frac{m g R}{2}$
C $- \frac{m g R}{3}$
D $- \frac{m g R}{4}$
Question 3 - Select One
A remote-sensing satellite of earth revolves in a circular orbit at a hight of $0.25 \times 10^{6} m$ above the surface of earth. If earth's radius is $6.38 \times 10^{6} m$ and $g = 9.8 m s^{- 2}$ , then the orbital speed of the satellite is
A $6.67 k m s^{- 1}$
B $7.76 k m s^{- 1}$
C $8.56 k m s^{- 1}$
D $9.13 k m s^{- 1}$

Recommended Questions

Home
Ask Doubt
Profile