A ray falls on a prismABC(AB=BC)and travels as shown in adjoining figure.The minimum refraction index of the prism material should be -
To find the minimum refractive index of the prism material, we can follow these steps:
Step 1: Understand the Geometry of the Prism
Given that the prism ABC has sides AB = BC, we can infer that it is an isosceles prism. The light ray is incident on face AC and undergoes total internal reflection at point D on face AB.
Step 2: Identify the Incident Angle
Since the ray is incident on face AB at point D, we note that the angle of incidence (i) at this point is 45 degrees. This is important because total internal reflection occurs when the angle of incidence is greater than the critical angle.
Step 3: Apply Snell's Law at Point D
At point D, we can apply Snell's Law, which states:
n1sin(i)=n2sin(r)
Where:
- n1 is the refractive index of the denser medium (the prism),
- n2 is the refractive index of the rarer medium (air, which is approximately 1),
- i is the angle of incidence (45 degrees),
- r is the angle of refraction.
Since the ray is undergoing total internal reflection, we can say that the angle of refraction r is 90 degrees (the ray is refracted along the boundary).
Step 4: Substitute Values into Snell's Law
Substituting the known values into Snell's Law:
nsin(45∘)=1sin(90∘)
Since sin(90∘)=1:
nsin(45∘)=1
Step 5: Solve for the Refractive Index
We know that sin(45∘)=√22:
n⋅√22=1
Now, solving for n:
n=2√2=√2
Step 6: Find the Minimum Refractive Index
The minimum refractive index of the prism material is:
n=√2≈1.414
Final Answer
Thus, the minimum refractive index of the prism material should be √2 or approximately 1.414.
---
Given that the prism ABC has sides AB = BC, we can infer that it is an isosceles prism. The light ray is incident on face AC and undergoes total internal reflection at point D on face AB.
Since the ray is incident on face AB at point D, we note that the angle of incidence (i) at this point is 45 degrees. This is important because total internal reflection occurs when the angle of incidence is greater than the critical angle.
At point D, we can apply Snell's Law, which states:
n1sin(i)=n2sin(r)
Where:
- n1 is the refractive index of the denser medium (the prism),
- n2 is the refractive index of the rarer medium (air, which is approximately 1),
- i is the angle of incidence (45 degrees),
- r is the angle of refraction.
Substituting the known values into Snell's Law:
nsin(45∘)=1sin(90∘)
Since sin(90∘)=1:
nsin(45∘)=1
We know that sin(45∘)=√22:
n⋅√22=1
Now, solving for n:
n=2√2=√2
The minimum refractive index of the prism material is:
n=√2≈1.414
Thus, the minimum refractive index of the prism material should be √2 or approximately 1.414.
Similar Questions
Find the angle of deviation suffered by the light ray shown in figure. The refractive index mu = for the prism material.
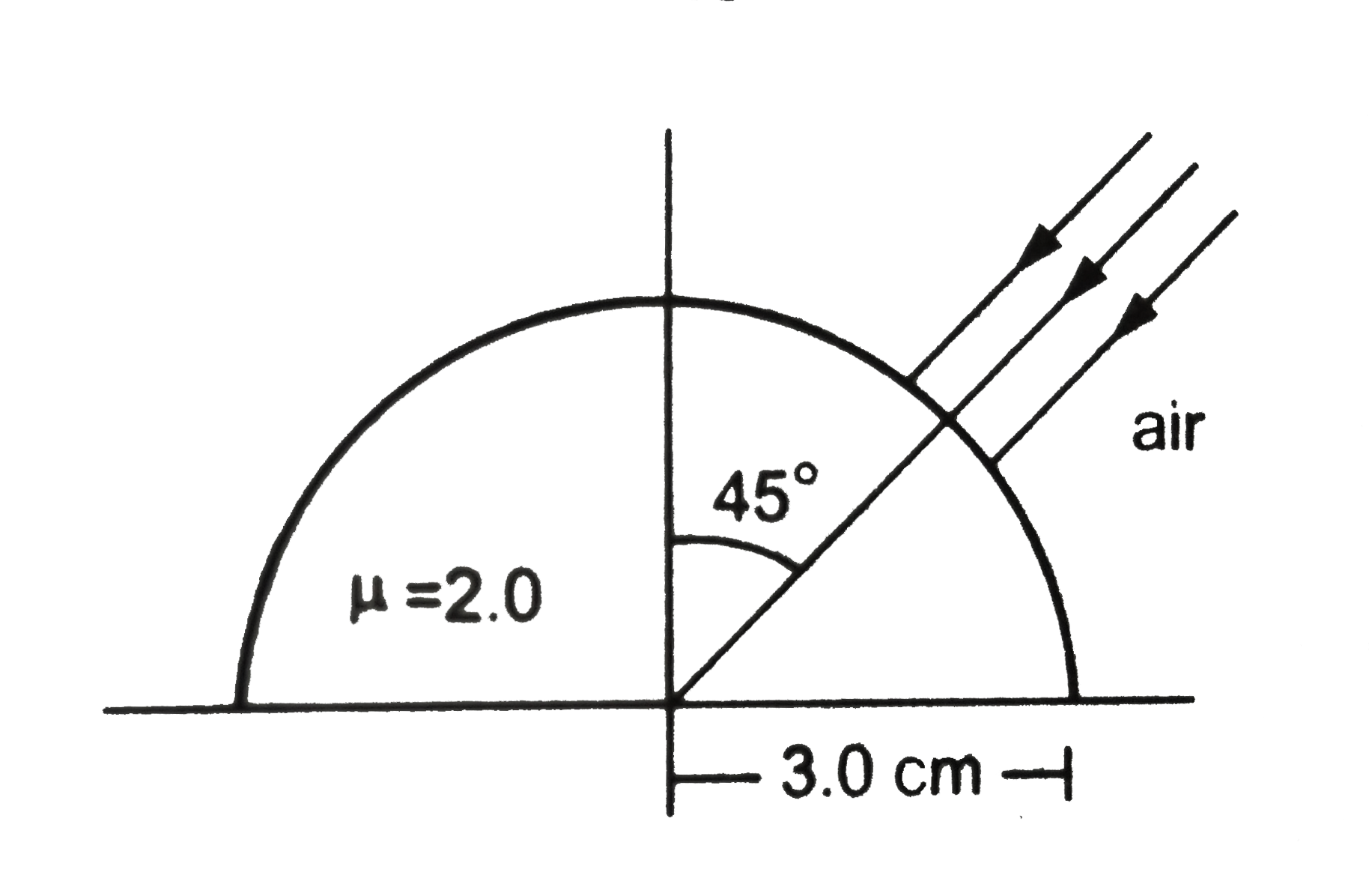
View SolutionA ray of light falling at an angle of 50∘ is refracted through a prism and suffers minimum deviation. The angle of the prism is 60∘. Find the angle of minimum deviation and refraction index of the material of the prism.
View Solution
Knowledge Check
A ray of light incident normally on an isosceles right angled prism travels as shown in the figure. The least value of the refractive index of the prism must be
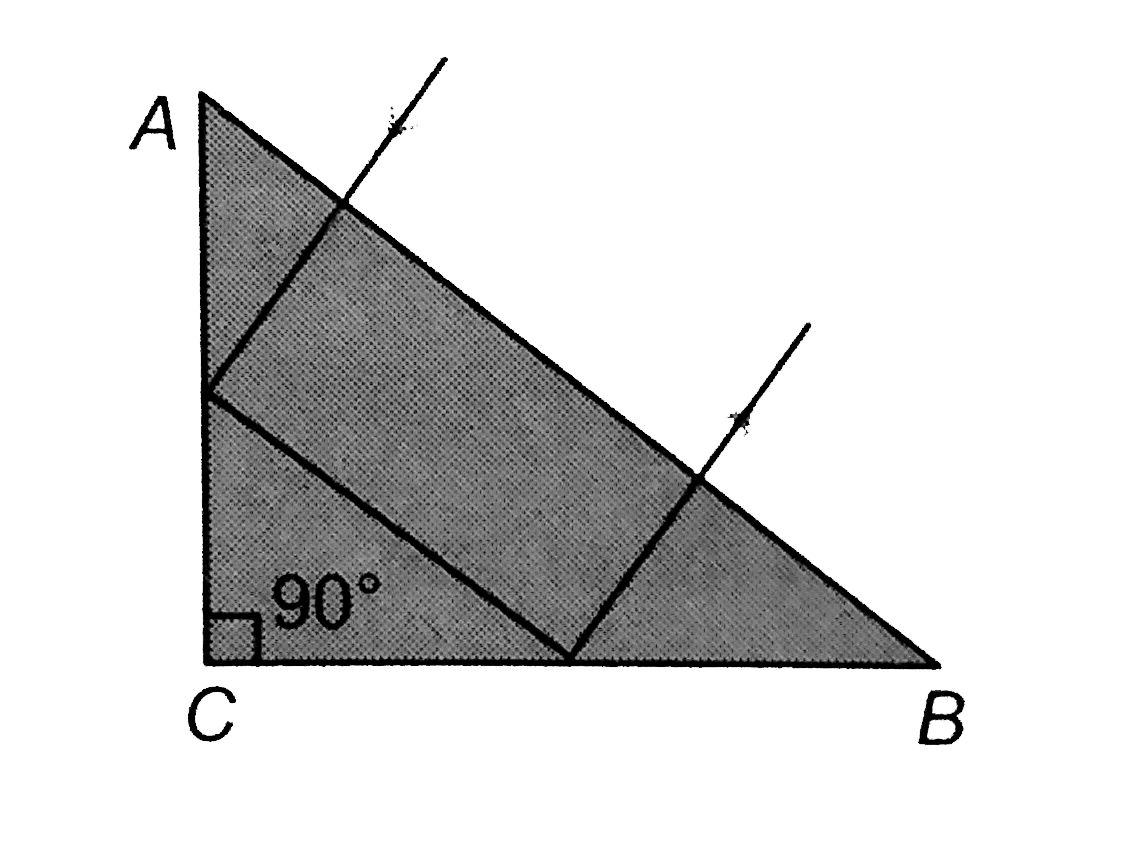 A√2B√3C1.5D2.0
A√2B√3C1.5D2.0
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, thenAThe angle of emergence θ2 of the ray is sin−2(58)BThe angle of emergence θ2 of the ray is sin−1(54√3)CThe angle of emerrgence θ2 of the ray is sin−1(73√4)DTotal internal reflection will not occur at P if the refractive index of water increases to a value greater than 52√3 by dissolving some substance.Find the net deviation produced in the incident ray for the optical instrument shown in figure. (Take refractive index of the prism material as 2.)
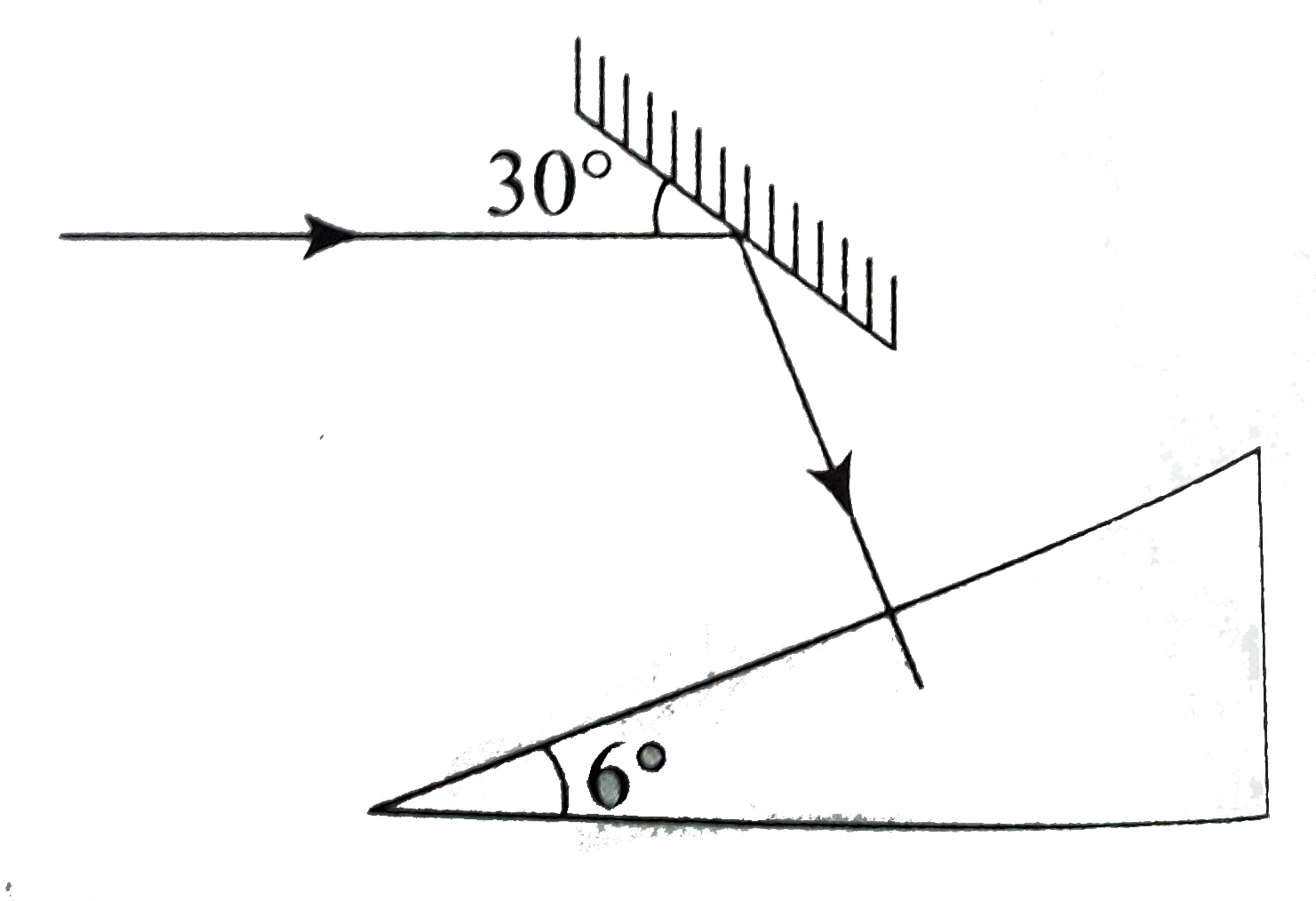 A66∘CWB66∘ACWC54∘ACWD54∘CW
A66∘CWB66∘ACWC54∘ACWD54∘CW
The angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘ . The refractive index of the prism material is
View SolutionA ray of light falls on an equilateral prism ABC as shown. Face AC of the prism is polished.

What is the refractive index μ of the material of the prims so that when the ray falls on face BC (after reflecting from AC) it makes an angle 60∘ with it.?
View SolutionA ray OP of monochromatic light is incident on the face AB of prism ABCD mear vertex B at an incident angle of 60degree (see figure). If the refractive index of the material of the prism is √3, which of the following is (are) are correct?

View SolutionWhen a ray of light falls on a prism of angle 48∘ , it suffers minimum deviation. Refractive index of the material of prism is 1.6. The angle of incidence is nearly
View SolutionThe angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘. The refractive index of prism material is
View Solution
