An opaque cylindrical tank with an open top has a diameter fo3.00mand is completely filled with water .When the settign sun reaches an angle of 37∘above the horizon,sunlight ceases to illuminate any part of the bottom of thetank .How deep is the tank?
The correct Answer is:4m
To find the depth of the cylindrical tank, we can use the geometry of the situation along with some trigonometric principles.
1. Understand the Geometry:
The cylindrical tank has a diameter of 3.00 m, which means the radius r is:
r=3.00m2=1.50m
2. Identify the Angle of Incidence:
The angle of the sun above the horizon is given as 37∘. This angle will help us determine how far the sunlight can penetrate into the tank.
3. Draw a Diagram:
Visualize a right triangle formed by the radius of the tank, the depth of the tank h, and the line of sunlight hitting the water surface. The angle at the water surface is 37∘.
4. Use Trigonometry:
In the right triangle, the tangent of the angle can be expressed as:
tan(37∘)=oppositeadjacent=hr
where h is the depth of the tank and r is the radius of the tank.
5. Substitute the Known Values:
We can now substitute the radius r=1.50m into the equation:
tan(37∘)=h1.50m
6. Calculate tan(37∘):
Using a calculator or trigonometric table, we find:
tan(37∘)≈0.7536
7. Solve for h:
Rearranging the equation gives:
h=1.50m⋅tan(37∘)≈1.50m⋅0.7536≈1.1304m
8. Final Result:
The depth of the tank is approximately:
h≈1.13m
The cylindrical tank has a diameter of 3.00 m, which means the radius r is:
r=3.00m2=1.50m
The angle of the sun above the horizon is given as 37∘. This angle will help us determine how far the sunlight can penetrate into the tank.
Visualize a right triangle formed by the radius of the tank, the depth of the tank h, and the line of sunlight hitting the water surface. The angle at the water surface is 37∘.
In the right triangle, the tangent of the angle can be expressed as:
tan(37∘)=oppositeadjacent=hr
where h is the depth of the tank and r is the radius of the tank.
We can now substitute the radius r=1.50m into the equation:
tan(37∘)=h1.50m
Using a calculator or trigonometric table, we find:
tan(37∘)≈0.7536
Rearranging the equation gives:
h=1.50m⋅tan(37∘)≈1.50m⋅0.7536≈1.1304m
The depth of the tank is approximately:
h≈1.13m
Similar Questions
An opaque cylindrical tank with an open top has a diameter of 6.00m and is completely filled with water. When the setting sun reaches an angle of 37∘ above the horizon, sunlight ceases to illuminate any part of the. bottom of the tank. The depth (in metre) of the tank is
View SolutionA cylinderical tank of height 0.4 m is open at the top and has a diameter 0.16m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5×10−3m in its bottom.
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical tank of height H is open at the top end and it has a radius r. Water is filled in it up to a height of h. The time taken to empty the tank through a hole of radius r' in its bottom is
A√2hgr2r'2B√2Hgr2r'2C√hHDnone of these - Question 2 - Select One
The figure shows the commonly observed decrease in diameter of a water stream as it falls from a tap. The tap has internal diameter D0 and is connected toa large tank of water. The surface of the water is at a height b above the end of the tap.
By considering the dynamics of a thin "cylinder" of water in the steam answer the following: (ignore any reistance to the flow and any effects of surface tansion, given ρw= density of water)
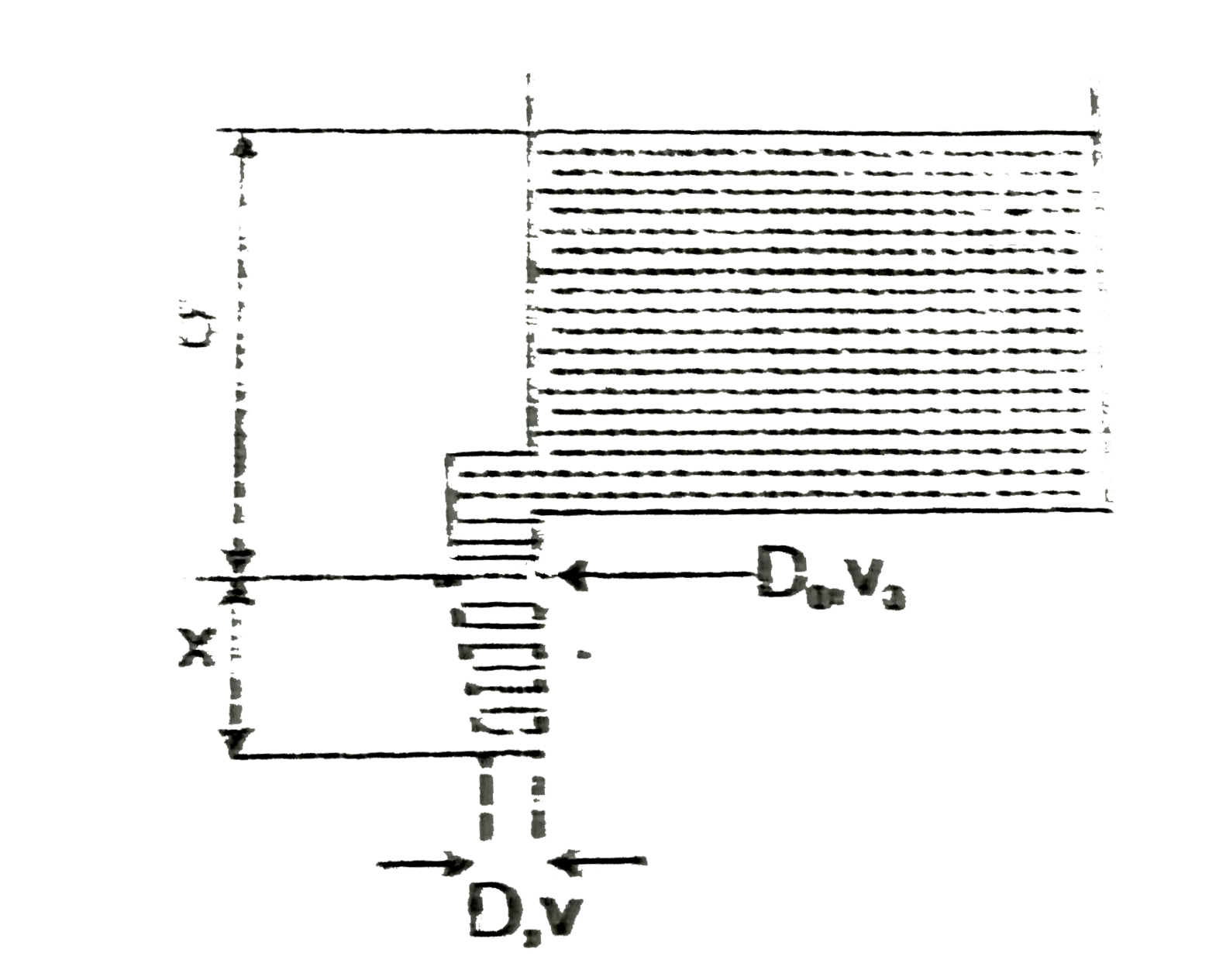
A student observes after setting up this experiment that for a tap with D0=1cm at x=0.3m the stream diameter D=0.9cm. The heights b of the water above the tap in this case will be:A5.7cmB57cmC27cmD2.7cm
A cylindrical tank of height 2 m is open at the top and has a radius 50 cm. Water is filled in it upto a height 1.75 m. Calculate how long it will take to empty the tank through a hole of radius 0.05 cm in its bottom.
View Solution_S01_053_Q01.png)
A large cylinderical tank of cross-sectional area 1m2 is filled with water . It has a small hole at a height of 1 m from the bottom. A movable piston of mass 5 kg is fitted on the top of the tank such that it can slide in the tank freely. A load of 45 kg is applied on the top of water by piston, as shown in figure. The value of v when piston is 7 m above the bottom is (g=10m/s2)
(a). √120m/s
(b). 10m/s
(c). 1m/s
(d). 11m/sView SolutionAn empty cylindrical tank having diameter 5 m is filled with water through a hose pipe having radius 25 cm. If pressure at the bottom of the container increases at a rate of 103Pa s−1, calculate the speed of water flowing through the hose pipe.
(Take g 10 m s−2)View Solution
Bottom of a cylindrical container is made of a thin equiconvex lens having bottom side silvered as shown in the figure. The container is completely filled by water. Consider an object in water at a point on the vertical axis of the lens at a height h=4m from the bottom. when we from top in water two images of the point O coicides with each other. (given μlens=1.5,μwater=43) The radius of curvature (in m) of the lens is.View SolutionIn Fig. an open tube of length L = 2.3 m and crosssectional area A = 9.2 cm2 is fixed to the top of a cylindrical barrel of diameter D = 1.2 m and height H = 2.3 m. The barrel and tube are filled with water to the top of the tube). Calculate the ratio of the hydrostatic force on the bottom of the barrel to the gravitational force on the water contained in the barrel. Why is that ratio not equal to 1.0? (You need not consider the atmospheric pressure.)
 View Solution
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)
 View Solution
View Solution

