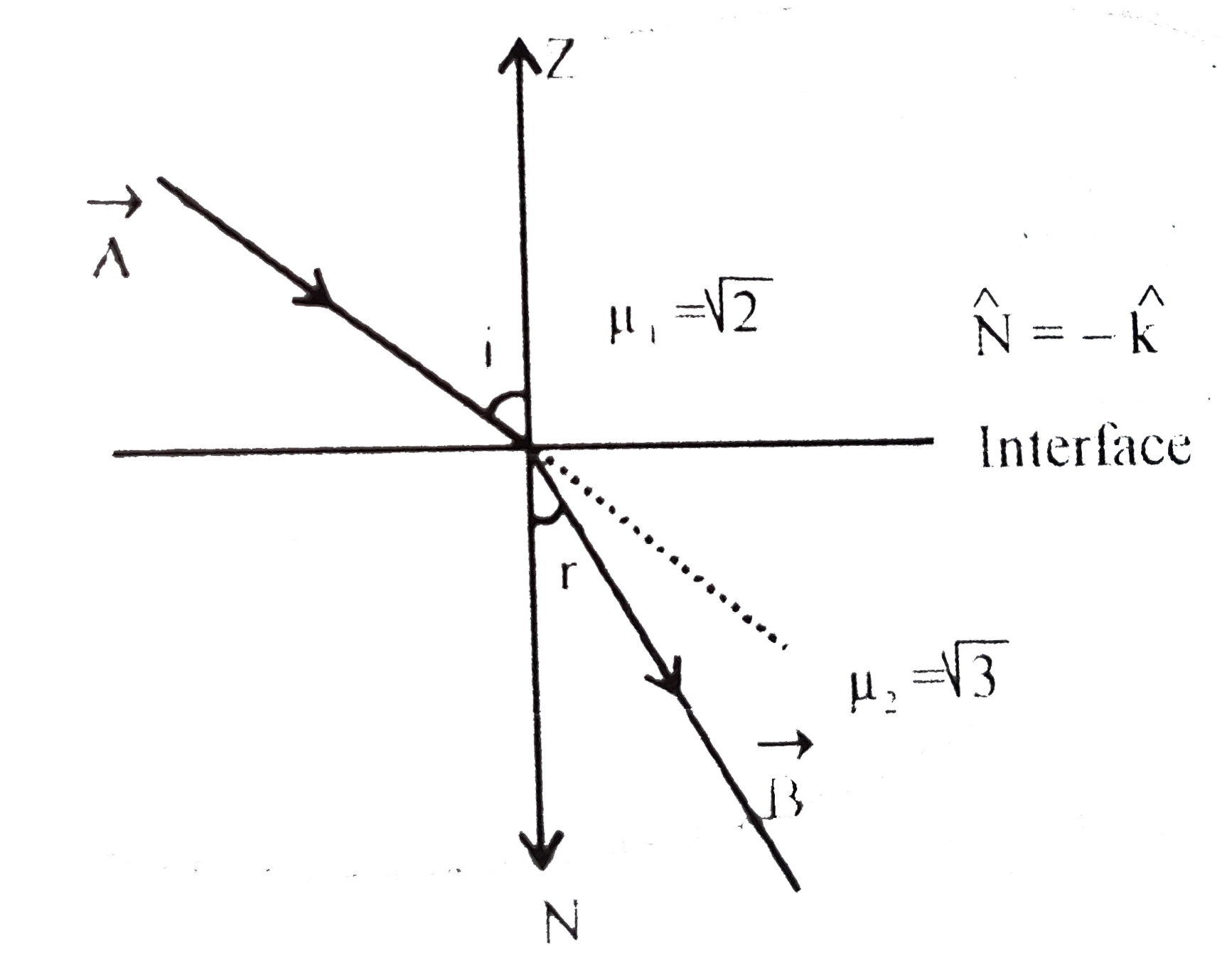
Let the x-z plane be the boundary between two transparent media. Medium 1 in $z \geq 0$ has a refractive index of $\sqrt{2}$ and medium 2 with $z < 0$ has a refractive index of $\sqrt{3}$ . A ray of light in medium 1 given by the vector $\to A = 6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 ˆ k$ is incident on the plane of separation. The angle of refraction in medium 2 is:

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\to r = \frac{3}{5 \sqrt{2}} ˆ i + \frac{2 \sqrt{2}}{5} ˆ j - \frac{1}{\sqrt{2}} ˆ k (angle of incidence = 60^{\circ}; r = 45^{\circ}$

For angle of incidence
$(\to A . ˆ N) = A cosi$
$cos i = \frac{(6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 ˆ k) (- ˆ k)}{\sqrt{{(6 \sqrt{3})}^{2} + (8 {\sqrt{3}}^{2}) + {(- 10)}^{2}}}$
$cos i = \frac{10}{20} \Rightarrow cos i \frac{1}{2}$
$i = 60^{\circ}$ From the law of refraction
$μ_{1} sin i = μ_{2} sin r$
$\sqrt{2} {sin 60}^{\circ} = \sqrt{3} sin r$
$\sqrt{2} \times \frac{\sqrt{3}}{2} = \sqrt{3} sin r$
$r = 45^{\circ}$
Due to refraction only normal conponents changes
$\to B = 6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - z ˆ k$
$\to B . ˆ N = B cos r$
$6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - z ˆ k . (- ˆ k) = \sqrt{6 {(\sqrt{3})}^{2} + {(8 \sqrt{3})}^{2} + {(- z)}^{2}} \times \frac{1}{\sqrt{2}}$
$\sqrt{2} z = \sqrt{300 + z^{2}}$
$2 z^{2} = 300 + z^{2} \Rightarrow z = 10 \sqrt{3}$
$\to B = 6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 \sqrt{3} ˆ k$
$\frac{6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 \sqrt{3} ˆ k}{10 \sqrt{6}}$
$ˆ B = \frac{3}{5 \sqrt{2}} ˆ i + \frac{2 \sqrt{2}}{5} ˆ j - \frac{1}{\sqrt{2}} ˆ k$

|

Updated on:21/07/2023

Class 11 PHYSICS RAY OPTICS

Similar Questions

Knowledge Check

Question 1 - Select One
Let the x-z plane be the boundary between two transparent media. Media 1 in $z \geq 0$ has refractive index of $\sqrt{2}$ and medium 2 with $z < 0$ has a refractive index of $\sqrt{3}$ . A ray of light in medium 1 given by the vector $\to A = 6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 ˆ k$ in incident on the plane of separation. The angle of refraction in medium 2 is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$
Question 2 - Select One
Let the x-z plane be the boundary between two transparent media . Medium 1 in $z \leq 0$ has a refrative index of $\sqrt{2}$ and medium 2 with $z < 0$ has a refracticve index of $\sqrt{3}$ A ray of light in medium 1 given by the vector $\to A = 6 \sqrt{3} ˆ i + 8 \sqrt{8} ˆ j - 10 ˆ k$ is incident on the plane of separation . The angle of refraction in medium 2 is
A $40^{\circ}$
B $60^{\circ}$
C $75^{\circ}$
D $30^{\circ}$
Question 3 - Select One
The $x - y$ plane is the boundary between two transparent media. Medium-1 with $z \leq 0$ has a refractive index $\sqrt{2}$ and medium -2 with $z \leq 0$ has a refractive index $\sqrt{2}$ . A ray of light in medium -1 given by vector $A = \sqrt{3} ˆ i - ˆ k$ is incident on the plane of separation. The unit vector in the direction of the refracted ray in medium-2 is
A $\frac{1}{\sqrt{2}} (ˆ k - ˆ i)$
B $\frac{1}{\sqrt{2}} (ˆ i + ˆ j)$
C $\frac{1}{\sqrt{2}} (ˆ i - ˆ k)$
D $\frac{1}{\sqrt{2}} (ˆ i + ˆ k)$

Recommended Questions

Home
Ask Doubt
Profile