A meniscus lens is made of a material of refractive index .Both its surfaces have radii of curvature .It has two different media of refractive indices and respectively ,on its two sides (See figure) .Calcualte its focal length for ,when light is incidence on it as shown
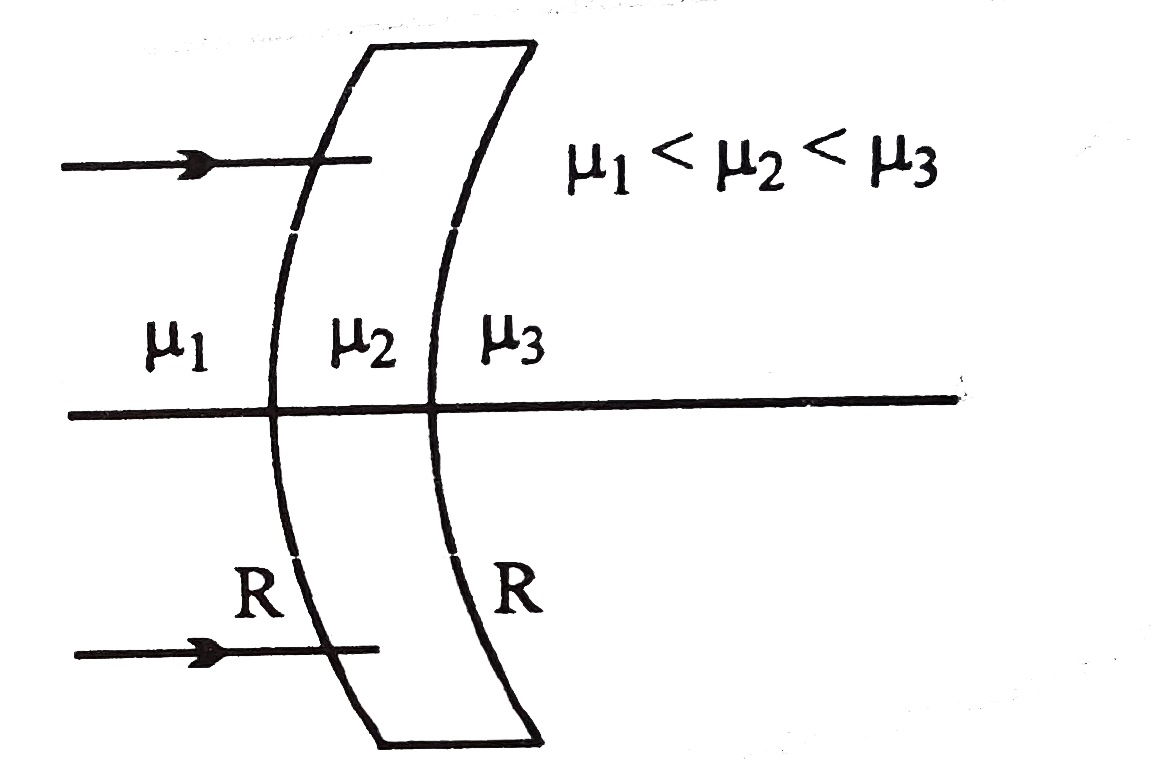
The correct Answer is:
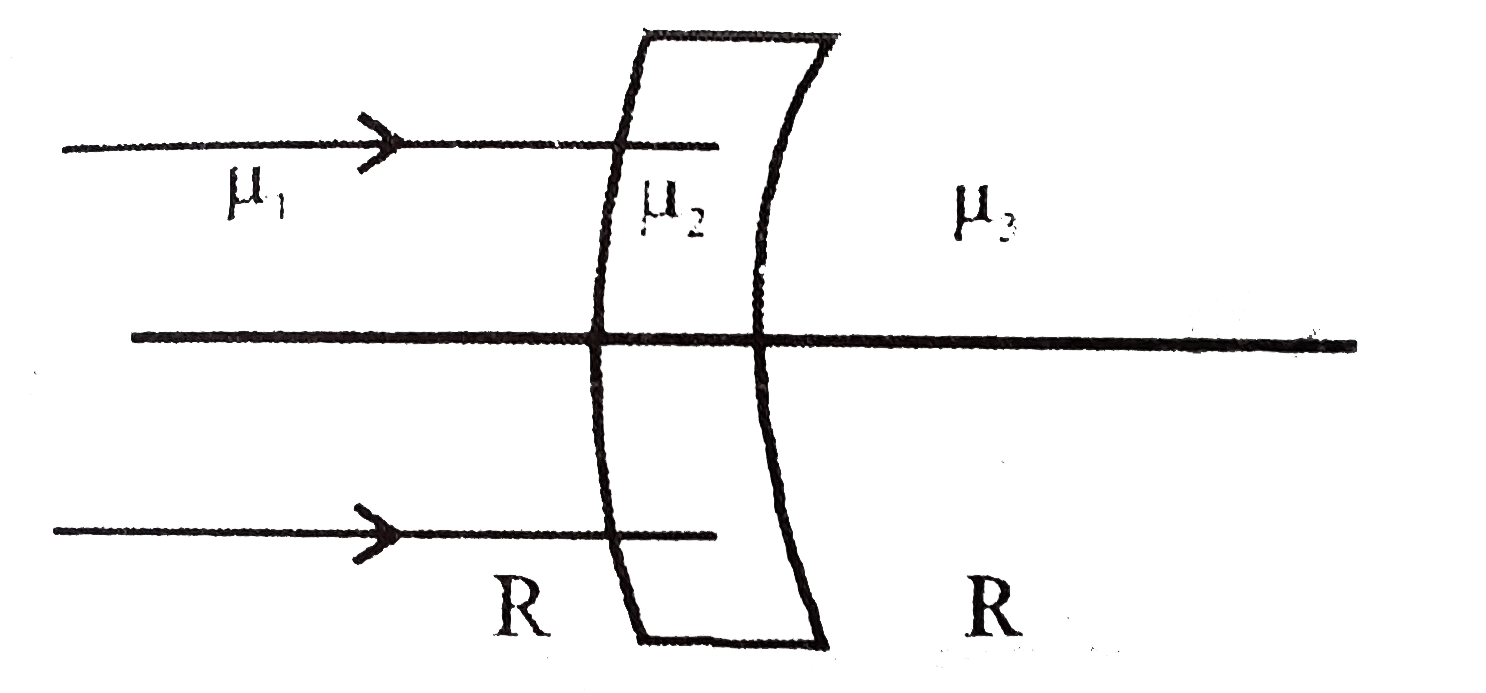
this image will act as object for second refraction.
Similar Questions
Knowledge Check
A convex lens (with material of refractive index of 3/2) has two surfaces of equal radii of curvature R. The magnitude of its focal length is
AR2BRC2RDzeroA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
Af∝(μ2−μ1)Bf∝μ1(μ2−μ1)Cf∝(μ2+μ1)Df∝1(μ2+μ1)The length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
Aμ1d1+μ2d2Bμ1d2+μ2d1Cd1d3μ1μ2Dd1+d2μ3μ2
A thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA thin glass lens of refractive index μ2=1.5 behaves as an interface between two media of refractive indices μ1=1.4andμ3=1.6 respectively. Determine the focal length of the lens for the shown arrangement of radius of curvature of both surfaces 20cm.
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
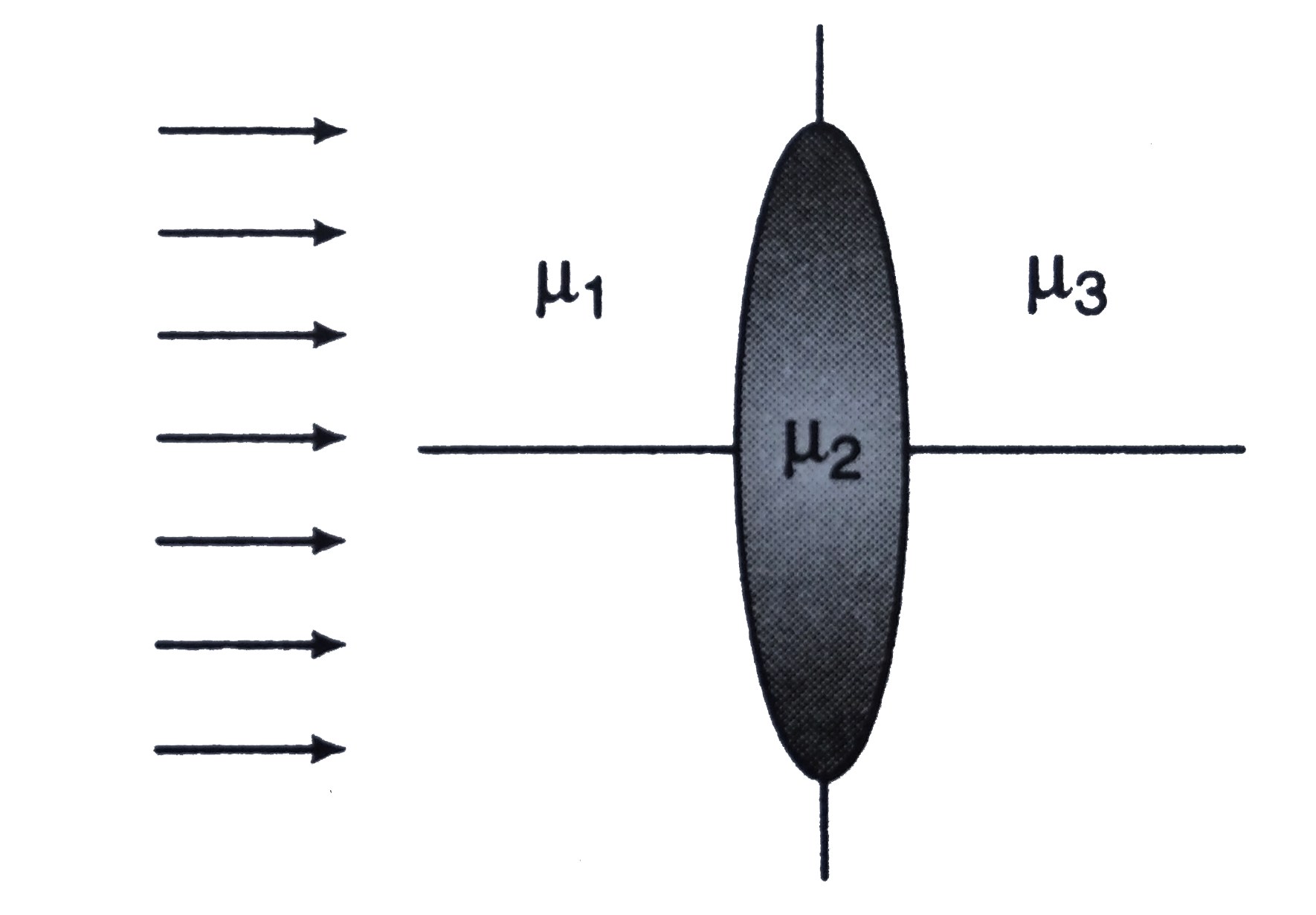
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
View Solution
