A capacitor is filled with two dielectrics of same dimensions, but of dielectric constants 2 and 3 respectively. Find the ratio of capacitances in the two arrangements shown in Fig.

As is clear from Fig.
C1=∈0AK1d/2,C2=∈0AK2d/2
These capacitors are joined in series, therefore equivalent capacity
C=C1C2C1+C2=(2∈0K1Ad)(2∈0K2Ad)2∈Ad(K1+K2)
C=2∈0AK1K2d(K1+K2) ...(i)
in Fig.
C3=∈0K1(A/2)d,C4=∈0K2(A/2)d
These capacitors are joined in parallel, therefore equivalent capacity
C'=C3+C4=∈0A2d(K1+K2) ....(ii)
Now, CC'=2∈0AK1K2d(K1+K2)×2d∈0A(K1+K2)
=4K1K2(K1+K2)2=4×2×3(2+3)2=2425
Similar Questions
The space between parallel plate capacitors is filled with four dielectrics of equal dimensions but of dielectric constants K1,K2,K3andK4 respectively. If K is the dielectric constant of a single dielectric that must be filled between capacitor plates to have the same capacitance between A and B. Then we must have

View SolutionThe area A of a parallel plate capacitor is divided into two equal, halves and filled with two media of dielectric constants K1andK2 respectively. The capacitance of the capacitor will be

View Solution
Knowledge Check
The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
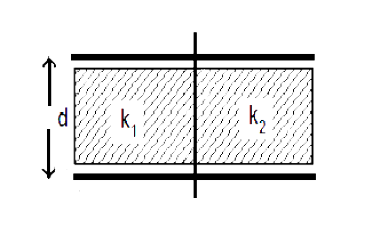 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)A parallel plate capacitor is filled with dielectrics. What is capacitance?
 A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)
A2K1K2K1+K2BK1K2K1+K2C2ε0Ad(K1K2K1+K2)D2ε0Ad(2K1+K22K1K2)A capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
A4Aε0dB4.8Aε0dC5Aε0dD2.4Aε0d
Capacitor has square plates of side l .Three dielectrics fill the space as shown (their dielectric constants are given).Find equivalent capacitance.
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be

View Solution
