Two charges of −4μCand+4μC are placed at the points A(1,0,4)andB(2,−1,5) location in an electric field →E=0.20ˆiV/cm. Calculate the torque acting on the dipole.
The correct Answer is:1.13×10−4N−m
To calculate the torque acting on the dipole formed by two charges of −4µC and +4µC, we will follow these steps:
Step 1: Identify the Position Vectors
The position vectors of the charges are given as:
- Charge −4µC at point A (1, 0, 4):
\(
\vec{r_1} = 1\hat{i} + 0\hat{j} + 4\hat{k}
\)
- Charge +4µC at point B (2, -1, 5):
\(
\vec{r_2} = 2\hat{i} - 1\hat{j} + 5\hat{k}
\)
Step 2: Calculate the Dipole Moment
The dipole moment \(\vec{p}\) is given by the formula:
\(
\vec{p} = q \cdot \vec{d}
\)
where \(\vec{d}\) is the displacement vector from the negative charge to the positive charge.
First, calculate \(\vec{d}\):
\(
\vec{d} = \vec{r_2} - \vec{r_1} = (2\hat{i} - 1\hat{j} + 5\hat{k}) - (1\hat{i} + 0\hat{j} + 4\hat{k}) = (2-1)\hat{i} + (-1-0)\hat{j} + (5-4)\hat{k} = 1\hat{i} - 1\hat{j} + 1\hat{k}
\)
Now, substituting \(q = 4 \times 10^{-6} C\):
\(
\vec{p} = 4 \times 10^{-6} \cdot (1\hat{i} - 1\hat{j} + 1\hat{k}) = 4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}
\)
Step 3: Electric Field Vector
The electric field vector is given as:
\(
\vec{E} = 0.20\hat{i} \text{ V/cm} = 20\hat{i} \text{ V/m}
\)
Step 4: Calculate the Torque
The torque \(\vec{\tau}\) acting on the dipole in an electric field is given by:
\(
\vec{\tau} = \vec{p} \times \vec{E}
\)
Substituting the values of \(\vec{p}\) and \(\vec{E}\):
\(
\vec{\tau} = (4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}) \times (20\hat{i})
\)
Using the properties of the cross product:
\(
\vec{\tau} = 4 \times 10^{-6} \times 20 (\hat{i} \times \hat{i}) - 4 \times 10^{-6} \times 20 (\hat{j} \times \hat{i}) + 4 \times 10^{-6} \times 20 (\hat{k} \times \hat{i})
\)
Since \(\hat{i} \times \hat{i} = 0\), we have:
\(
\vec{\tau} = 0 - 4 \times 10^{-6} \times 20 (-\hat{k}) + 4 \times 10^{-6} \times 20 \hat{j}
\)
\(
= 80 \times 10^{-6} \hat{k} + 80 \times 10^{-6} \hat{j} = 8 \times 10^{-5} \hat{j} + 8 \times 10^{-5} \hat{k}
\)
Step 5: Magnitude of the Torque
The magnitude of the torque vector is given by:
\(
|\vec{\tau}| = \sqrt{(8 \times 10^{-5})^2 + (8 \times 10^{-5})^2} = 8 \times 10^{-5} \sqrt{2}
\)
\(
= 8\sqrt{2} \times 10^{-5} \text{ Nm}
\)
Calculating the numerical value:
\(
|\vec{\tau}| \approx 1.13 \times 10^{-4} \text{ Nm}
\)
Final Answer
The torque acting on the dipole is approximately:
\(
\boxed{1.13 \times 10^{-4} \text{ Nm}}
\)
The position vectors of the charges are given as:
- Charge −4µC at point A (1, 0, 4):
\(
\vec{r_1} = 1\hat{i} + 0\hat{j} + 4\hat{k}
\)
- Charge +4µC at point B (2, -1, 5):
\(
\vec{r_2} = 2\hat{i} - 1\hat{j} + 5\hat{k}
\)
The dipole moment \(\vec{p}\) is given by the formula:
\(
\vec{p} = q \cdot \vec{d}
\)
where \(\vec{d}\) is the displacement vector from the negative charge to the positive charge.
\(
\vec{d} = \vec{r_2} - \vec{r_1} = (2\hat{i} - 1\hat{j} + 5\hat{k}) - (1\hat{i} + 0\hat{j} + 4\hat{k}) = (2-1)\hat{i} + (-1-0)\hat{j} + (5-4)\hat{k} = 1\hat{i} - 1\hat{j} + 1\hat{k}
\)
\(
\vec{p} = 4 \times 10^{-6} \cdot (1\hat{i} - 1\hat{j} + 1\hat{k}) = 4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}
\)
The electric field vector is given as:
\(
\vec{E} = 0.20\hat{i} \text{ V/cm} = 20\hat{i} \text{ V/m}
\)
The torque \(\vec{\tau}\) acting on the dipole in an electric field is given by:
\(
\vec{\tau} = \vec{p} \times \vec{E}
\)
\(
\vec{\tau} = (4 \times 10^{-6}\hat{i} - 4 \times 10^{-6}\hat{j} + 4 \times 10^{-6}\hat{k}) \times (20\hat{i})
\)
\(
\vec{\tau} = 4 \times 10^{-6} \times 20 (\hat{i} \times \hat{i}) - 4 \times 10^{-6} \times 20 (\hat{j} \times \hat{i}) + 4 \times 10^{-6} \times 20 (\hat{k} \times \hat{i})
\)
\(
\vec{\tau} = 0 - 4 \times 10^{-6} \times 20 (-\hat{k}) + 4 \times 10^{-6} \times 20 \hat{j}
\)
\(
= 80 \times 10^{-6} \hat{k} + 80 \times 10^{-6} \hat{j} = 8 \times 10^{-5} \hat{j} + 8 \times 10^{-5} \hat{k}
\)
The magnitude of the torque vector is given by:
\(
|\vec{\tau}| = \sqrt{(8 \times 10^{-5})^2 + (8 \times 10^{-5})^2} = 8 \times 10^{-5} \sqrt{2}
\)
\(
= 8\sqrt{2} \times 10^{-5} \text{ Nm}
\)
\(
|\vec{\tau}| \approx 1.13 \times 10^{-4} \text{ Nm}
\)
The torque acting on the dipole is approximately:
\(
\boxed{1.13 \times 10^{-4} \text{ Nm}}
\)
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS7videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
Two charges 4μCand−4μC are placed at (−3,0,0)and(3,0,0) cm respectively in an external field given by E=9×106r2Cm−2 , Find the energy of the system in this external field.
A−2.4JB2.4JC0D−1.4J - Question 2 - Select One
Electric dipole of moment →p=pˆi is kept at a point (x, y) in an electric field →E=4xy2ˆi+4x2yˆj. Find the magnitude of force acting on the dipole.
A4py√y2+2x2B2py√y2+4x2C4py√y2+4x2D2py√y2+2x2 - Question 3 - Select One
A magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
A175ˆk Nm,B75ˆiNmC150ˆiNmD25√37ˆiNm,
Two charges of ±1000μC are separated by 2mm. This dipole so formed is held at an angle of 30∘ with a uniform electric field of 15×104N/C. Calculate the torque acting on the dipole.
View SolutionTwo charges one +5μC, and another −5μC ,are placed 1 mm apart . Calculate the dipole moment.
View SolutionTwo charges 2μCand−2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotenital surface of the system.
(b) What is the direction of the electric field at every point on this surface ?View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
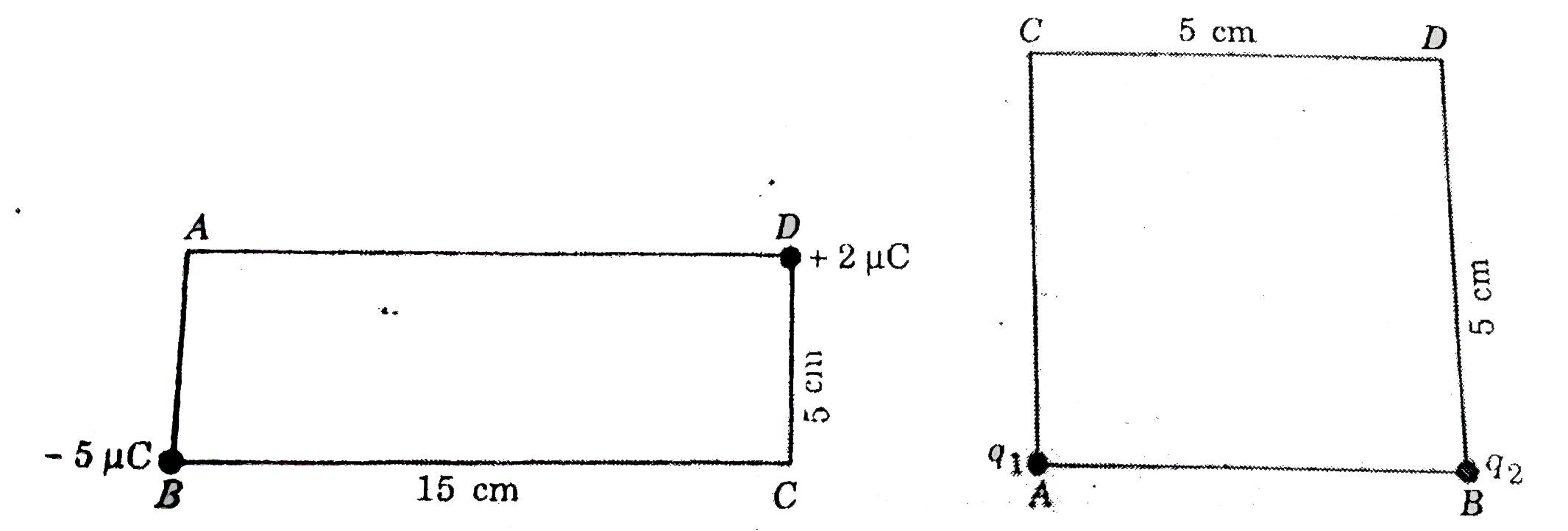 View Solution
View SolutionA magnet of magnetic moment 50ˆiA−m2 is placed along the x-axis in a magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the magnet is
View Solution

