Two capacitors have a capacitance of 5μF when connected in parallel and 1.2μF when connected in series. Calculate their capacitance.
The correct Answer is:2μF,3μF
To solve the problem of finding the capacitance of two capacitors when they are connected in parallel and in series, we can follow these steps:
Step 1: Set up the equations based on the given conditions
Let the capacitances of the two capacitors be C1 and C2.
1. When connected in parallel, the total capacitance is given by:
Cparallel=C1+C2=5μF(Equation 1)
2. When connected in series, the total capacitance is given by:
1Cseries=1C1+1C2⟹Cseries=C1C2C1+C2=1.2μF(Equation 2)
Step 2: Express C2 in terms of C1
From Equation 1, we can express C2 as:
C2=5−C1(Equation 3)
Step 3: Substitute C2 in Equation 2
Substituting Equation 3 into Equation 2:
Cseries=C1(5−C1)C1+(5−C1)=C1(5−C1)5=1.2
Step 4: Solve for C1
Now, we can rearrange the equation:
C1(5−C1)=1.2×5
C1(5−C1)=6
5C1−C21=6
Rearranging gives us a quadratic equation:
C21−5C1+6=0
Step 5: Factor the quadratic equation
Factoring the quadratic equation:
(C1−2)(C1−3)=0
Step 6: Find the values of C1
Setting each factor to zero gives:
C1−2=0⇒C1=2μF
C1−3=0⇒C1=3μF
Step 7: Find C2
Using Equation 3 to find C2:
1. If C1=2μF:
C2=5−2=3μF
2. If C1=3μF:
C2=5−3=2μF
Thus, the capacitances of the two capacitors are:
C1=2μFandC2=3μF
Final Answer:
The capacitances of the two capacitors are 2μF and 3μF.
---
Cparallel=C1+C2=5μF(Equation 1)
1Cseries=1C1+1C2⟹Cseries=C1C2C1+C2=1.2μF(Equation 2)
C2=5−C1(Equation 3)
Cseries=C1(5−C1)C1+(5−C1)=C1(5−C1)5=1.2
C1(5−C1)=1.2×5
C1(5−C1)=6
5C1−C21=6
Rearranging gives us a quadratic equation:
C21−5C1+6=0
(C1−2)(C1−3)=0
C1−2=0⇒C1=2μF
C1−3=0⇒C1=3μF
1. If C1=2μF:
C2=5−2=3μF
C2=5−3=2μF
C1=2μFandC2=3μF
The capacitances of the two capacitors are 2μF and 3μF.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Two capacitors of equal capacitance when connected in series hae net capacitance C1 and when connected in parallel have net capacitance C2 what is the value of C1/C2?
View SolutionThree capacitors of equal capacitance, when connected in series have net capacitance C1, and when connected in parallel have net capacitance C2. What is the value of C1/C2?
View Solution
Knowledge Check
Two capacitors each of capacity 2μF are connected in parallel. This system is connected in series with a third capacitance of 12μF capacity . The equivalent capacity of the system will be
A16μFB13μFC4μFD3μFTwo capacitors of capacitances 3μFand5μF respectively are connected in parallel and this combination is connected in series with a third capacitor of capacitance 2μF. A potential difference of 100 V is applied across the entire combination. The charge and the potential difference across the third capacitor is
A100μC,40VB100μC,80VC160μC,40VD160μC,80VTwo identical capacitors when joined in series have an effective capacitance of 3μF. When connected in parallel, the effective capacitance becomes 12μF. What is the capacitance of each capacitor ?
A6μFB3μFC12μFD9μF
Two capacitors of capaciatance 3μFand5μF respectively are joined in parallel and the combination is connected in series with a third capacitor of capacitance 2μF. What is the resultant capacitane.
View SolutionThree capacitors of capacitances 2μF,2μFand4μF are connected to a battery of 10V as shown in the figure. Calculate the effective capacitance of the circuit and charge on each capacitor.
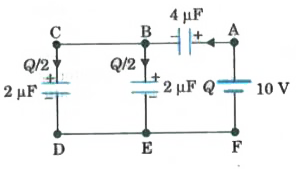
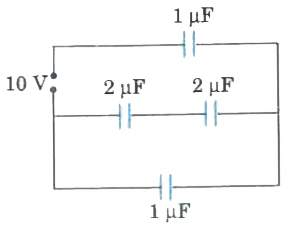
View SolutionFour capacitors of capacitances 2 μF and 1μF are connected across a battery of 10V as shown in the figure (q). Calculate the net capacitance of the combination and net charge across each capacitor.
View SolutionTwo capacitors when connected in parallel are equivalent to 6μF and when the same are connected in series then the equivalent becomes 1.5 μF. Calculate the individual capacitances.
View SolutionTwo capacitors of capacitances 4μF and another two of 5μF are connected as shown in the given figure (f). Calculate the effective capacitance across points A and B.
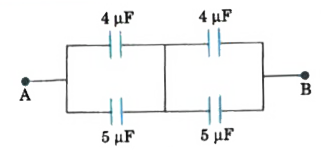
View Solution
