A 20μF capacitors is charged by a 30V d.c supply and then connected across an uncharged 50μF capacitor. Calculate (i) the final potential diff. across the combinition (ii) initial and final energies.
The correct Answer is:8.57V;9×10−3J,2.57×10−3J
Here C1=20μF=20×10−6F
V1=30V,C2=50μF=50×10−6F.
V2=0,V=?
V=C1V1+C2V2C1+C2=20×10−6×30(20+50)10−6
=607V=8.57V
Initial energy, U1=12C1V21
=12(20×10−6)(30)2=90×10−3 joule
Finia energy, U2=12(C1+C2)V2
=12(20+50)10−6(607)2=2.57×10−3 joule
Loss of energy =U1−U2
=9×10−3−2.57×10−3=6.43×10−3J
This loss of energy appears in the form of heat and e.m. radiations.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS7videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
220 V, Hz is connected across a capacitor of 5μF. Calculate the effective current.
View SolutionA 80μF capacitor is charged by a 50V battery. The capacitor is disconnected from the battery and then connected across another uncharged 320μF capacitor. Calculate the charge on the second capacitor.
View Solution
Knowledge Check
- Question 1 - Select One
A capacity of capacity C1 is charged up to V volt and then connected to an uncharged capacitor of capacity C2. Then final potential difference across each will be
AC2VC1+C2B(1+C2C2)VCC1VC1+C2D(1−C2C1)V - Question 2 - Select One
A 20F capacitor is charged to 5V and isolated. It is then connected in parallel with an uncharged 30F capacitor. The decrease in the energy of the system will be
A25JB200JC125JD150J - Question 3 - Select One
A capacitor C1 is charged to a p.d.V. The charging battery is then removed and the capacitor is connected to an uncharged capacitor C2. The final p.d. across the combination is
AVC1C1+C2BVC2C1+C2CVC1C2C1+C2DVC1+C2
A100μF capacitor is charged o a potential difference of24V. It is connected to an uncharged capacitor of capaciance20μFWhat will be the new polential diffeernce across the 100 pF capacitor?
View SolutionA 4μF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2μF capacitor. How much electrostatic energy of the first capacitor is disspated in the form of heat and electromagnetic radiation ?
View SolutionA 10μF capacitor is charged to 15V. It is next connected in seties with an uncharged 5μf capacitor. The series cambination is finally connected across a 30V battery, as shown in. Find the new potential differnce across the 5μF and 10μF capacitors.
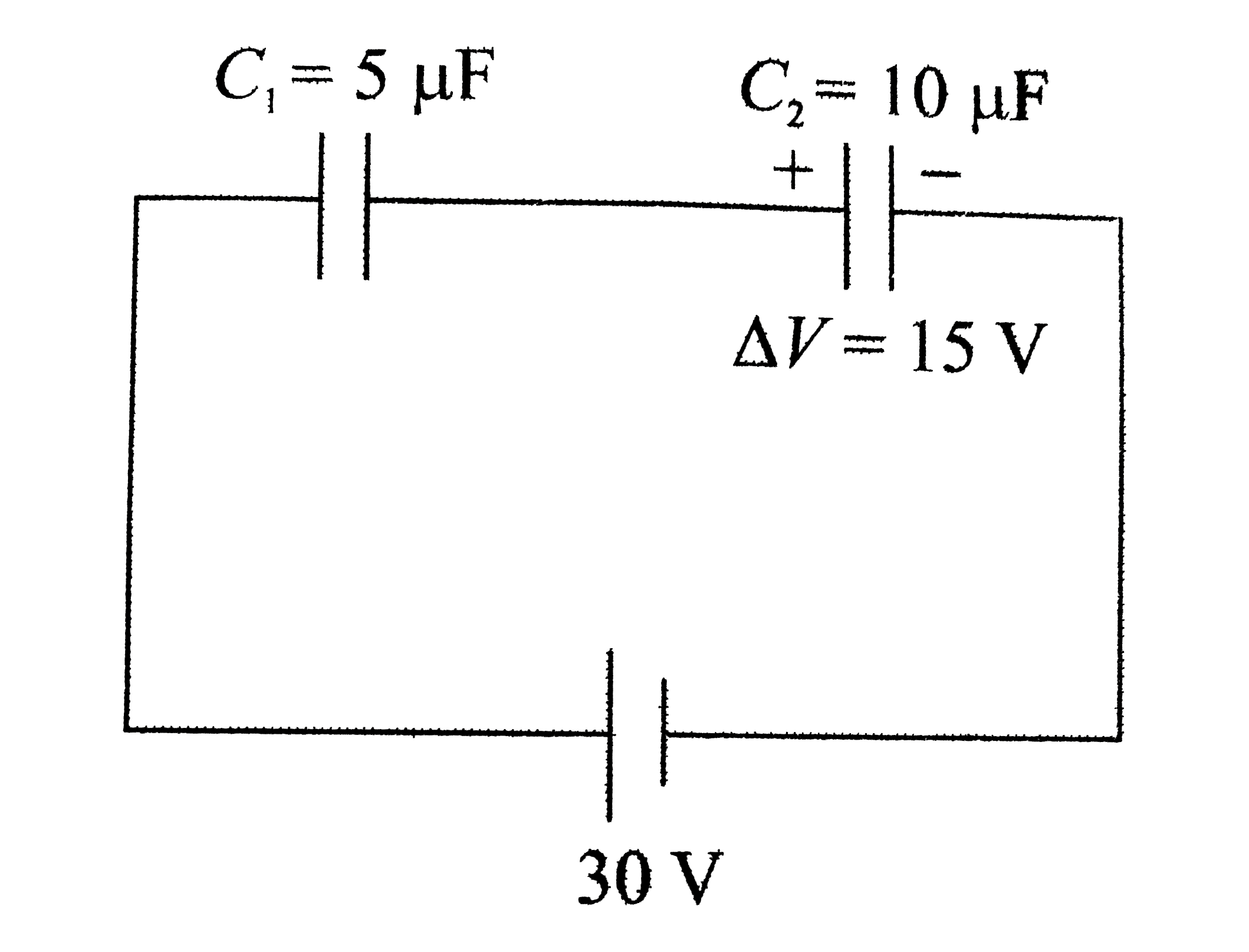 View Solution
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View Solution

