A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
−q4π2∈0r2ˆj
−q2π2∈0r2ˆj
q2π2∈0r2ˆj
q4π2∈0r2ˆj
The correct Answer is:C
Let λ be the linear charge desntiy on the semicirular ring. Then λ=q/πr. Take an element of the ring of length Δl as shown in Fig.
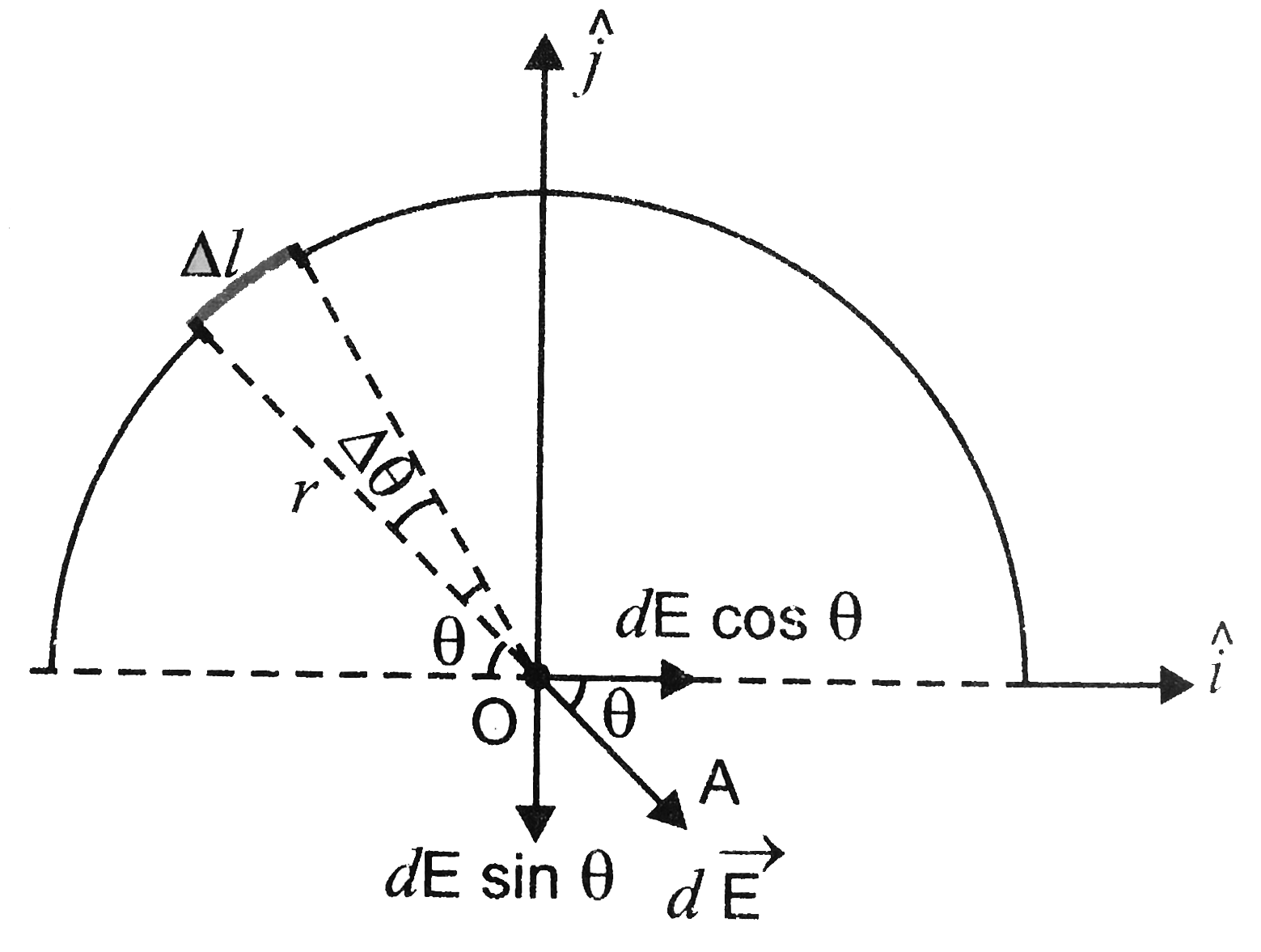
Charge on element, dq=λΔl=λ(rΔθ).
Elecatric field intensity at O due to charge on element is dE=14π∈0λrΔθr2 along OA
Two recentagular components of −→dEare dEcosθ along x-direction and dEsinθ along negative y-direction.If we find the electric field at Odue to charge on all other elements of the ring and resolve them into two recentagular components, we note that the components along X-direction cancel out in pairs and components along negative y-direction add up. Therefore, total electric field intensity at O due to charge on the entire semicircular ring is
→E=∫180∘0dEsinθ(−ˆj)
=∫180∘014π∈0lamndarΔθsinθr2(−ˆj)
=14π∈0λr[−cosθ]180∘9−ˆj0
=14π∈0λr[cos180∘−cos0∘]ˆj
=14π∈0(q/πr)r[−1−1]ˆj
=q2π2∈0r2ˆj
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS7videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
A ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionA non-conducting ring of radius r has charge q distributed unevenly over it. What will be the equivalent current if it rotates with an angular velocity Ω?
View Solution
Knowledge Check
- Question 1 - Select One
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it as shown in the figure. The net field →E at the center O is
 Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj
Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj - Question 2 - Select One
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32 - Question 3 - Select One
A small element l cut from a circular ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
AzeroBλl4πε0a2C∞Dλ4πεl
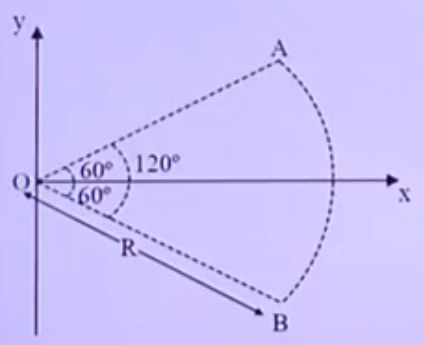
Figure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
 View Solution
View SolutionA thin wire carries a uniformly distributed charge Q = 3. 14nC along its length. The wire is bent in the form of a semi-circular arc of radius R = 1 m (without disturbing the charge distribution). Find the electric field at the center of curvature of the arc (in N/C).
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA thin wire ring of radius r has an electric charge q. What is the tension of the wire if a point charge q0 is placed at the ring's centre?
View SolutionAs shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is
 View Solution
View Solution

