The resistance between the terminal point A and B of the given infinitely long circuit will be
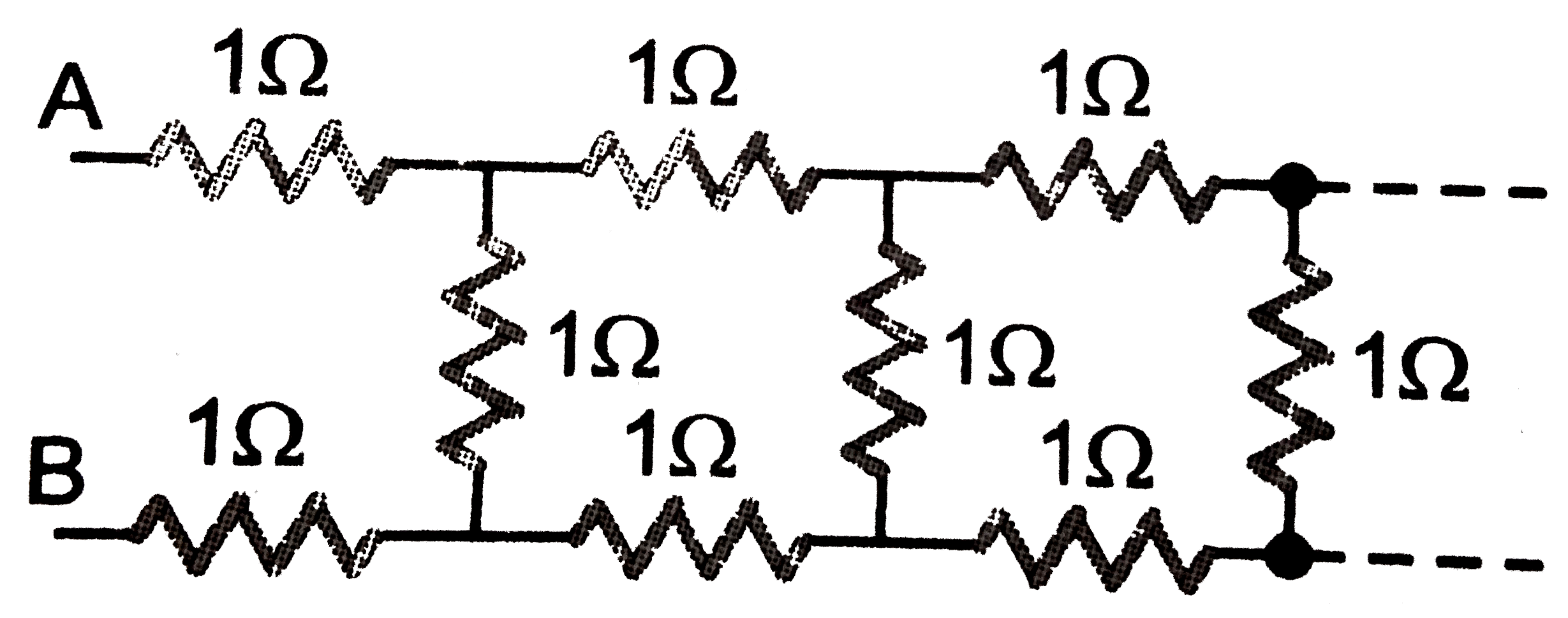
A
(√3−1)
B
(1−√3)
C
(1+√3)
D
(2+√3)
Video Solution
Text Solution
The correct Answer is:c
Ler x the equivalent resistance of infinite net work .Since the net work is infinite , the addition of one more unit of there terminals will not alter , the total resistance each the total resistance of network i.e. it appear alter, the total resistance of network, i.e., it should ne x. Therefore, the network would appear and in total resistance should remain x Effective resistance A and B is
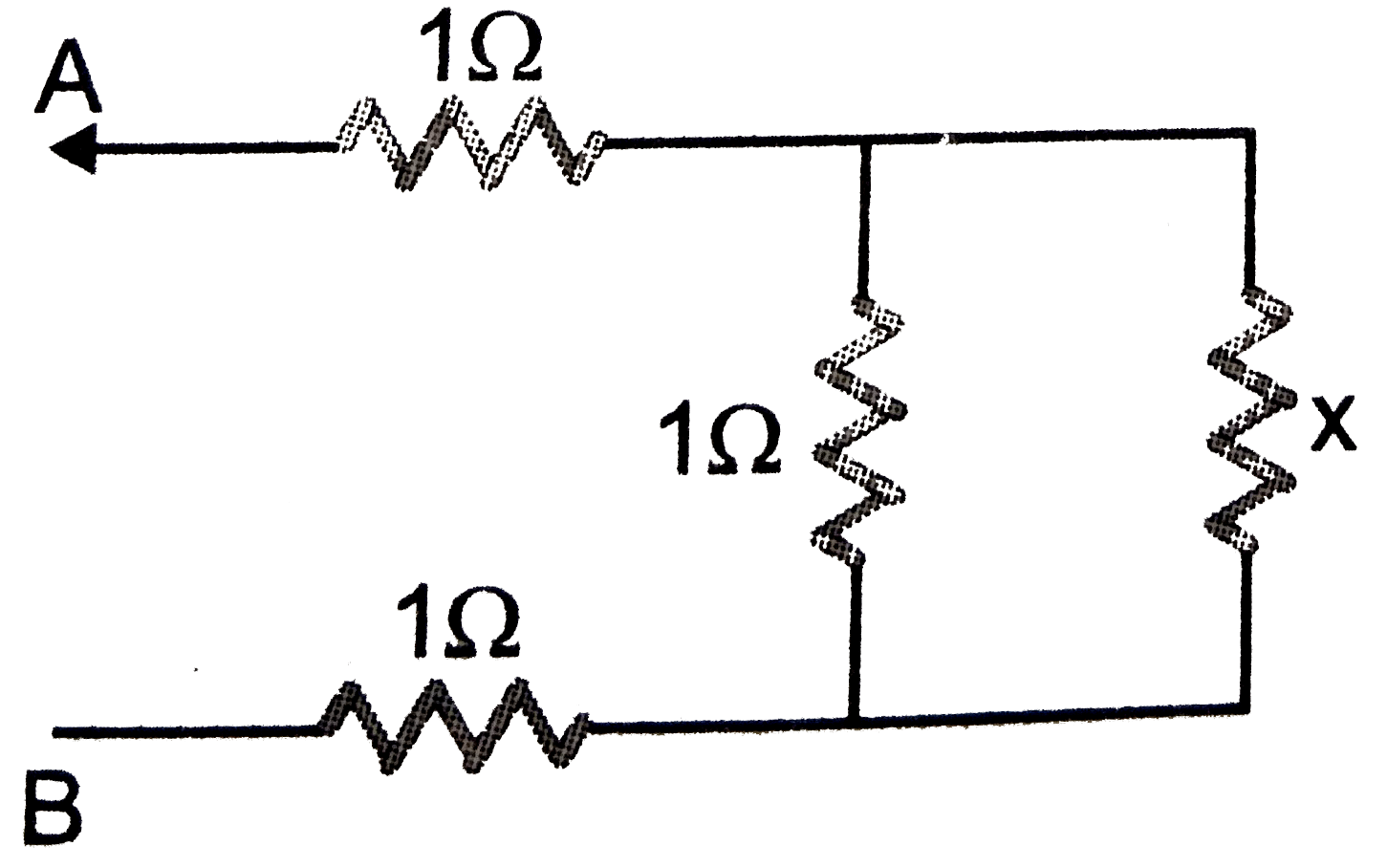
x=1+1×x1+x+1=2+x1+x
On siolving we get x=(1+√3)Ω
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Jee (main and advance)
Explore 4 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Interger Type
Explore 2 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Value based
Explore 2 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Knowledge Check
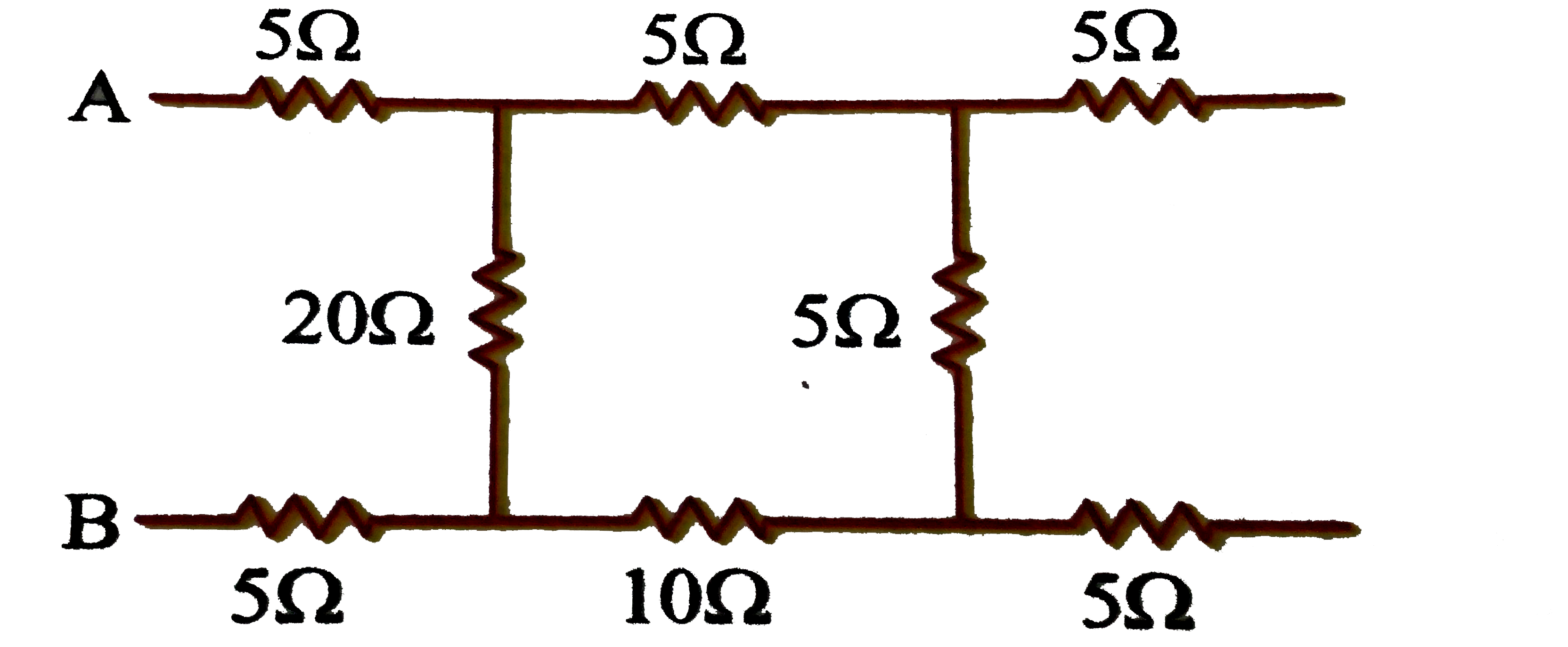
The resistance of the network between the terminals A and B isA30ΩB20ΩC50ΩD60ΩThe capacitance between the points A and B in the given circuit will be
 A1μFB2μFC3μFD4μF
A1μFB2μFC3μFD4μFWhat is equivalent resistance between the points A and B of an infinite network of resistance will be
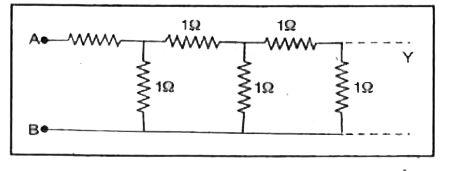 AinfiniteBzeroC2ΩD1+√52Ω
AinfiniteBzeroC2ΩD1+√52Ω
The equivalent resistance between points A and B in the given circuit is
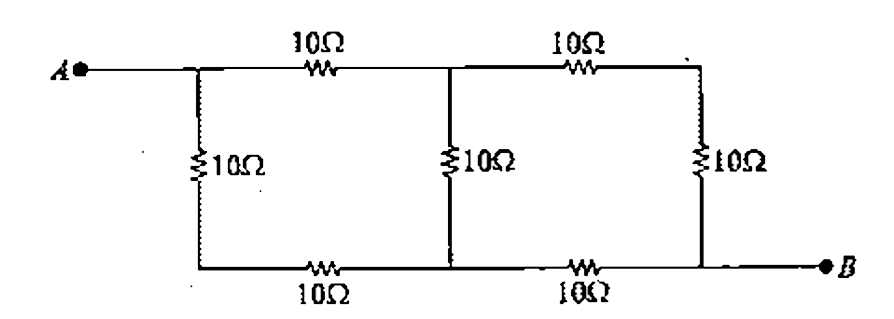
View SolutionWhat is the equivalent resistance between the terminal points A and B in the cirucit shown in figure-3.84
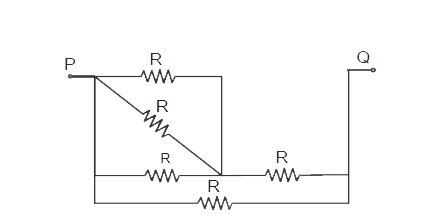
View SolutionThe equivalent resistance between the terminal point P and Q is 4Ω in the given circuit, then find out the resistance of R in ohms
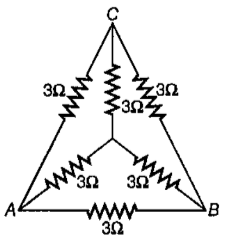
View SolutionFind the net resistance between point A and B in the circuit

View SolutionFind the equivalent resistance between the terminal points A and B in the network shown in the figure.
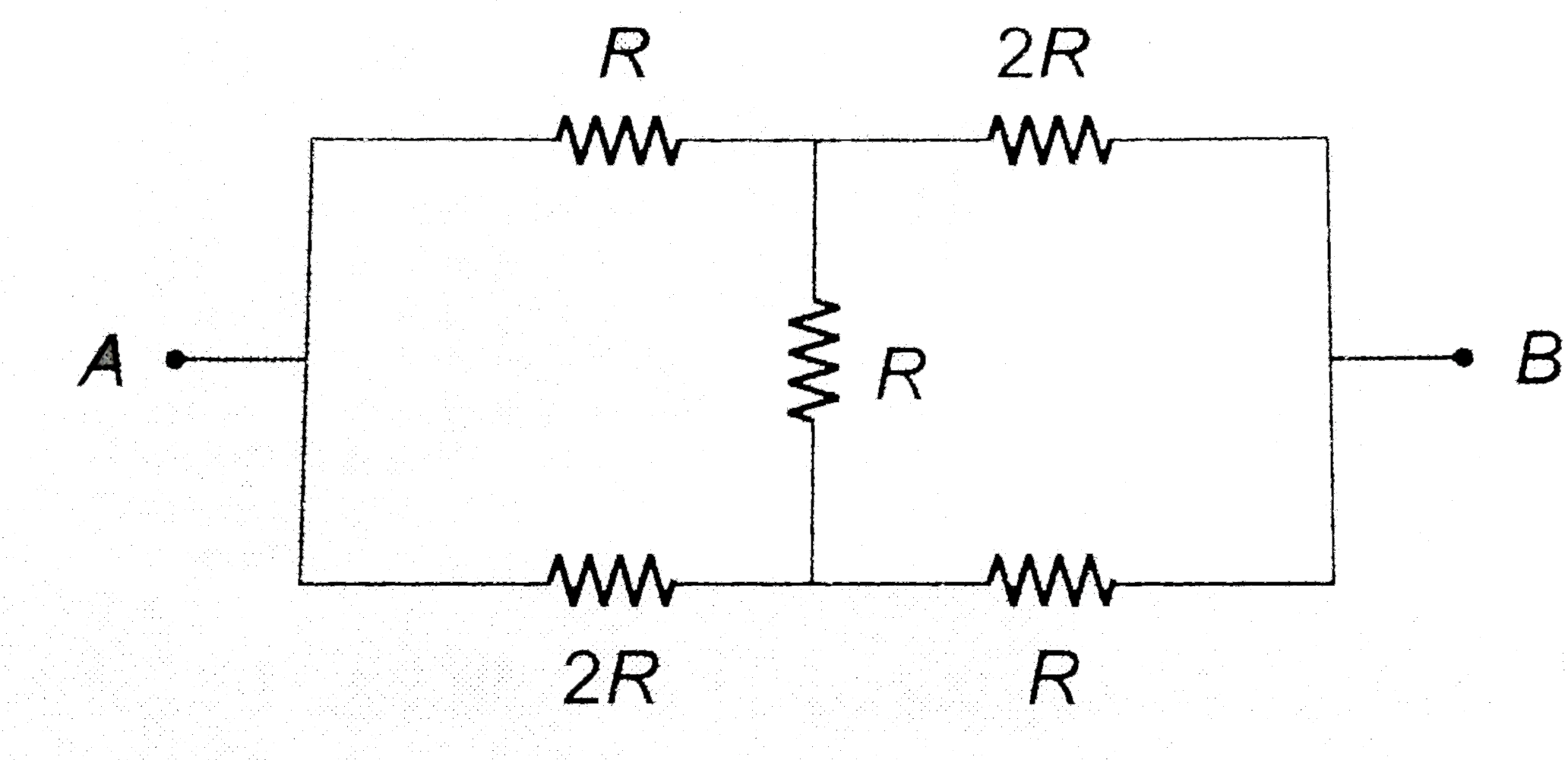 .
.
View Solution

