The charge flowing through a conductor varies with time as
q=8t−3t2+5t3
Find (i) the initial current (ii) time after which the current reaches a maximum value of current
The correct Answer is:(i)l=8A,(ii)0.2s,(iii)7.4A
Given q=8t−3t2+5t3
(i) current I=dqdt=8−6t+15t2…..(i)
When t=0I=8A
(ii) dIdt=−6+30t
For l to the maximum or minimum
dIdt=0or−6+30t=0ort=0.2s
(iii) putting this value of t in (i) we get
I=8−6×0.2+15(0.2)2=8−1.2+0.6=7.4A
As this value of l is less than at t=0, it will be minimum value , so minimum value of current =7.4A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Jee (main and advance)
4 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Interger Type
2 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Value based
2 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
The charge flowing in a conductor varies with time so q=2t−6t2+10t3
where qis in coloumn and r in second Find (i) the initial current (ii) the time after which the value of current reaches is maximum value (ii) the maximum or minimum value of current
View SolutionThe charge flowing in a conductor varies time as,
q=at−12bt2+16ct3
Where a,b,c are positive constants. Then, find (i) the initial current (ii) the time after which the value of current reaches a maximum value (iii) the maximum or minimum value of current.
View Solution
Knowledge Check
The charge flowing in a conductor varies with times as Q=at−bt2. Then, the current
Adecreases linearly with timeBreaches a maximum and then decreasesCfalls to zero at time t=a/2bDchanges at a rate - 2bThe charge q flowing in a conductor of uniform cross section, varies with time as q=αt−batat2. Then, the current
Adecreases linearly with timeBreaches a maximum and then decreasesCfalls to zero after a time t−α/2βDchanges at the rate-2βA change Q flowing through a conductor , beginning with time t=0, is given by Q=3t2+2t+. If the intensity of the current is the rate of change of Q w.r.t. t, then the intensity at the end of the fifth second is
A123 unitsB23 unitsC132 unitsD32 units
The charge flowing through a conducting wire with time t is given by the formula q=2t2+3t+1 (coulombs). Find the current i=dq/dt at the end of the 5th second.
View SolutionThe charge flowing throug a conductor beginning with time to=0 is given by the formula q=2t2+3t+1 (coulombs). Find the current i=dqdt at the end of the 5th seconds.
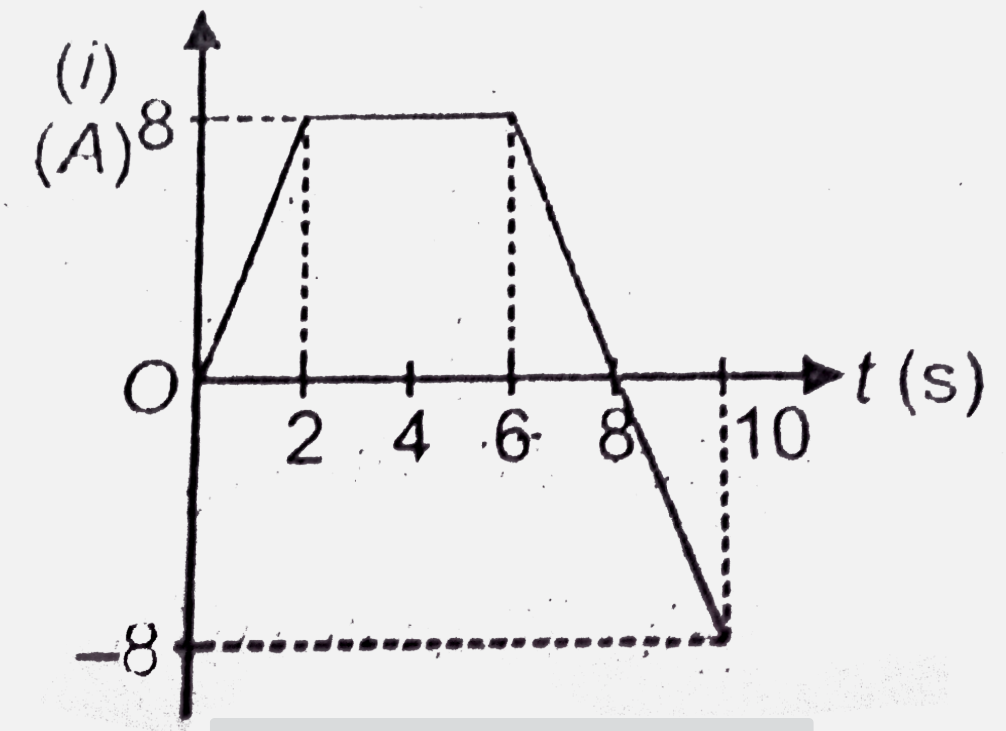
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionIf charge through a cross-section of a conductor at timetis q=2t2+3t+1. Find the current at t = 2s.
View SolutionThe current i through a wire varies with time t as shown in the fig. The effective (rms) value of the current is
View Solution
