Twelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
The correct Answer is:3.5Ω
To find the resistance between the current of the same edge of a cube formed by twelve identical wires, each with a resistance of 6Ω, we can follow these steps:
Step 1: Understand the Configuration
We have a cube with 12 edges, and each edge has a resistance of 6Ω. We need to find the equivalent resistance between two points (let's say points A and B) that are at the ends of one edge of the cube.
Step 2: Identify the Edge and Collapse Method
We will use the collapsing method to simplify the circuit. We will keep the edge AB (with resistance R=6Ω) intact and collapse the other edges into a simpler equivalent circuit.
Step 3: Analyze the Remaining Resistors
When we collapse the cube, the resistances connected to the edge AB will change. The resistors connected to the edge AB will be in parallel and series combinations.
- The two edges adjacent to AB will each have a resistance of 6Ω and will be in parallel with each other. The equivalent resistance of these two resistors is:
Rparallel=R2=62=3Ω
Step 4: Combine the Resistors
Now we have:
1. The resistance of edge AB: R=6Ω
2. The equivalent resistance of the two adjacent edges: Rparallel=3Ω
The two resistances (the intact edge and the equivalent of the two adjacent edges) are in series. Therefore, the total resistance Rtotal is:
Rtotal=R+Rparallel=6+3=9Ω
Step 5: Consider the Remaining Resistors
There are also two edges directly opposite to the edge AB. Each of these edges has a resistance of 6Ω and will also be in parallel with the previous combination. Therefore, we need to find the equivalent resistance of these remaining edges.
The total resistance of the two edges opposite to AB in parallel is:
Ropposite=R2=62=3Ω
Step 6: Final Combination
Now we have:
1. The resistance from the edge AB and the two adjacent edges: 9Ω
2. The resistance from the two opposite edges: 3Ω
These two resistances are in parallel:
1Rfinal=19+13
Calculating this gives:
1Rfinal=19+39=49
Thus,
Rfinal=94=2.25Ω
Step 7: Conclusion
The final equivalent resistance between the current of the same edge of the cube is:
Rfinal=2.25Ω
We have a cube with 12 edges, and each edge has a resistance of 6Ω. We need to find the equivalent resistance between two points (let's say points A and B) that are at the ends of one edge of the cube.
We will use the collapsing method to simplify the circuit. We will keep the edge AB (with resistance R=6Ω) intact and collapse the other edges into a simpler equivalent circuit.
When we collapse the cube, the resistances connected to the edge AB will change. The resistors connected to the edge AB will be in parallel and series combinations.
Rparallel=R2=62=3Ω
Now we have:
1. The resistance of edge AB: R=6Ω
2. The equivalent resistance of the two adjacent edges: Rparallel=3Ω
Rtotal=R+Rparallel=6+3=9Ω
There are also two edges directly opposite to the edge AB. Each of these edges has a resistance of 6Ω and will also be in parallel with the previous combination. Therefore, we need to find the equivalent resistance of these remaining edges.
Ropposite=R2=62=3Ω
Now we have:
1. The resistance from the edge AB and the two adjacent edges: 9Ω
2. The resistance from the two opposite edges: 3Ω
1Rfinal=19+13
1Rfinal=19+39=49
Thus,
Rfinal=94=2.25Ω
The final equivalent resistance between the current of the same edge of the cube is:
Rfinal=2.25Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Problems for Practice (A)
Explore 1 Video
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Twelve identical wires each of resistance 6Ω are arranged to from a skelence cube. A current of 40mA is led cube at the current and out at the diagonally opposite corner. Calculate the potential difference development across these current and the effective resistance of the network
View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View Solution
Knowledge Check
Twelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
A712rB127rC57rD125rTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩSix equal resistances, each 1Ω, are joined to form a network as showing figure Then the resistance between any two corners is
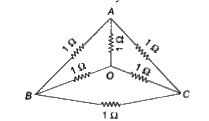 A0.5ΩB2ΩC1ΩD1.5Ω
A0.5ΩB2ΩC1ΩD1.5Ω
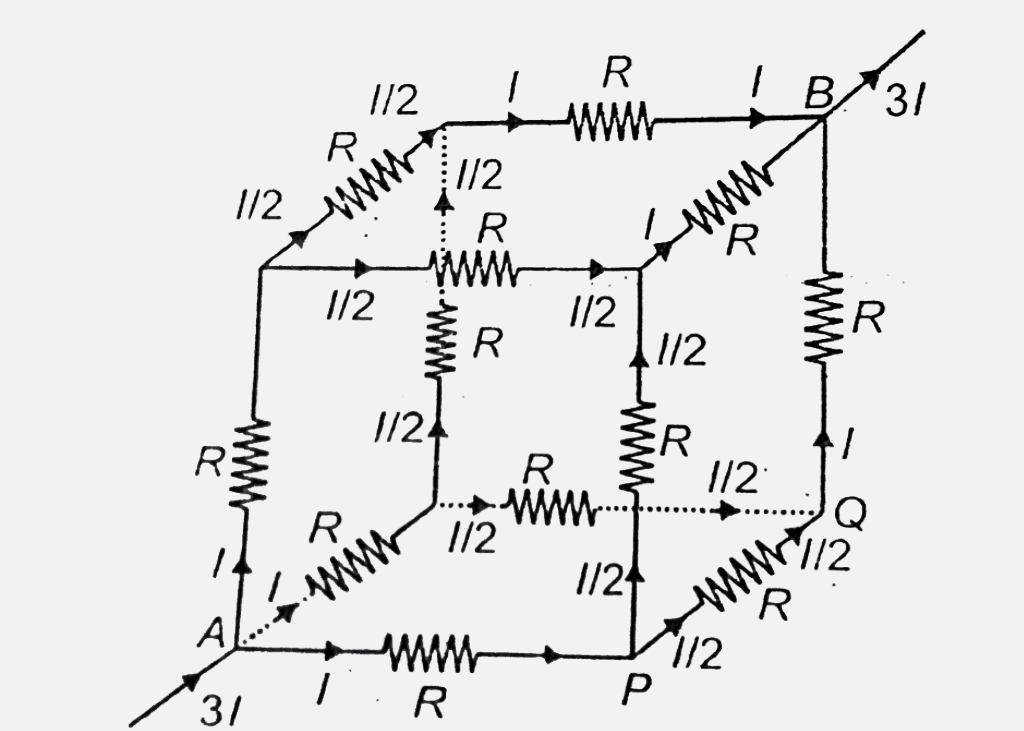
Tweve identical resistance each of resistance R are joined to form a cube as shown in figure.
Find resistance of the combination across AB
View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View SolutionEleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View Solution