A body of mass m is hauled from the Earth's surface by applying a force F varying with the height of ascent y as F=2(ay−1)mg, whera a is a positive constant. Find the work performed by this force and the increment of the body's potential energy in the gravitational field of the Earth over the first half of the ascent.
First, let us find the total height of ascent. At the beginning and the end of the path of velocity of the body is equal to zero, and therefore the increment of the kinetic energy of the body is also equal to zero. On the other hand, in according with work-energy theorem ΔT is equal to the algebric sum of the works. A performed by all the forces, i.e., by the force F and gravity, over this path. However, since ΔT=0 then A=0. Taking into account that the upward direction is assumed to coincide with the positve direction of the y-axis, we can write
A=h∫0(→F+m→g)⋅d→r=h∫0(Fy−mg)dy
=mgh∫0(1−2ay)dy=mgh(1−ah)=0.
whence h=1/a.
The work performed by the force F over the first half of the ascent is
AF=h/2∫0Fydy=2mgh/2∫0(1−ay)dy=3mg/4a.
The corresponding increment of the potential energy is
ΔU=mgh/2=mg/2a.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
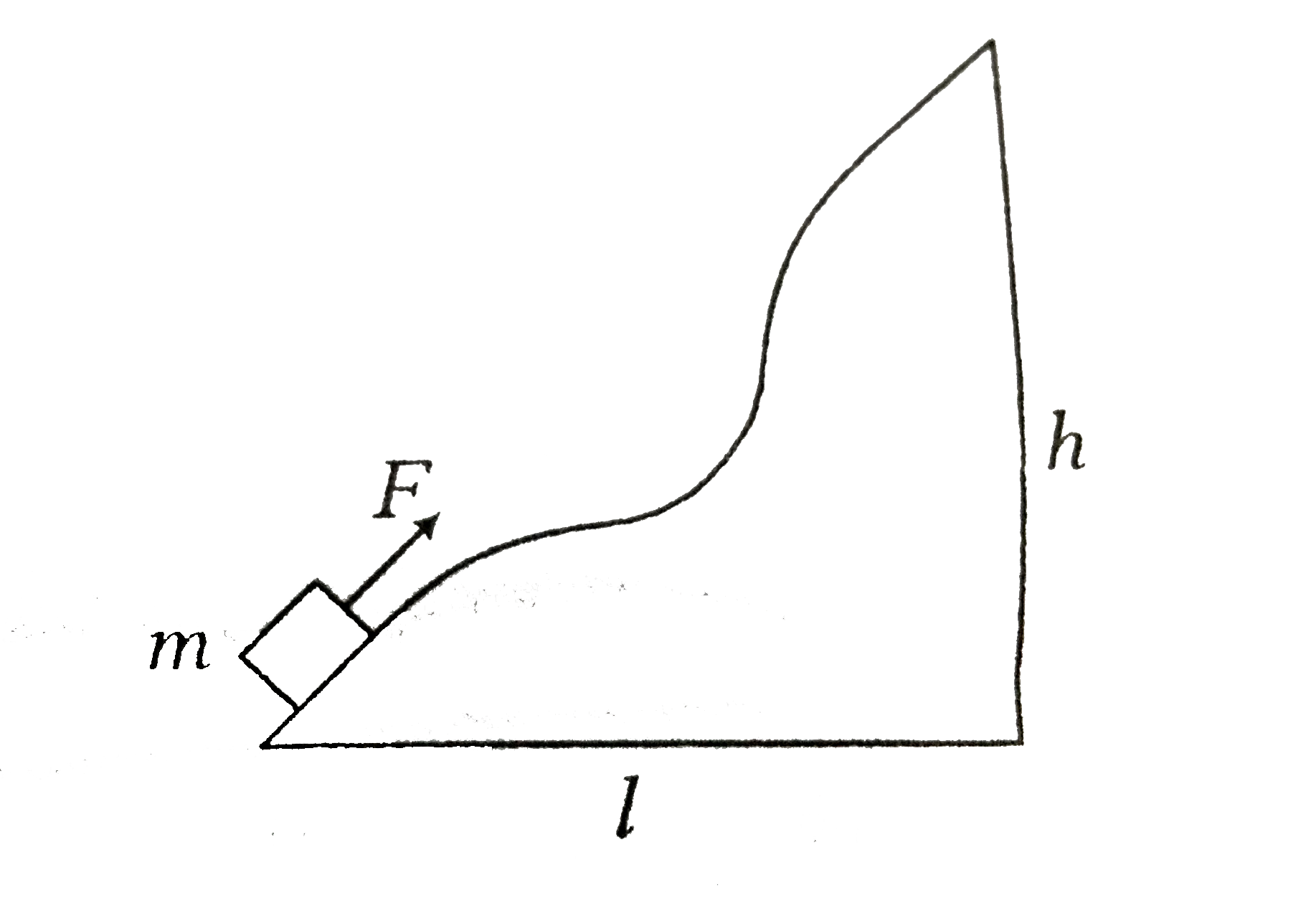
A body of mass m was slowly hauled up the hill (figure) by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base l, and the coefficient of friction k.
 View Solution
View SolutionA body of mass m is taken from the earth's surface to the height equal to twice the radius (R) of the earth.The change in potential energy of body will be
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m is placed on the earth surface is taken to a height of h=3R, then, change in gravitational potential energy is
AmgR4B2mgR3C3mgR4DmgR6 - Question 2 - Select One
A body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be
AmgRB12mgRC2mgRD14mgR - Question 3 - Select One
A body of mass m was slowly pulled up the hill by a force F which at each point was directed along the tangent of the trajectory. All surfaces aresmooth. Find the work performed by this force.
 AmglB−mglCmghDzero
AmglB−mglCmghDzero
A body of mass m was slowly hauled up the hill as shown in the fig. by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base is I and the coefficient ot friction is μ.
 . View Solution
. View SolutionA body of mass m was slowly hauled up the hill (figure) by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force, if the height of the hill is h, the length of its base l, and the coefficient of friction k.
 View Solution
View SolutionA force F=(y2+2y+5)N acts on a block in positive y- direction.Find the work done by this force during a displacement from y=-1m to y=+1m .
View SolutionIf a body of mass m is raised to height 2 R from the earths surface, then the change in potential energy of the body is (R is the radius of earth)
View SolutionA force given by the relation F=8t, acts on a body of mass 2kg, initialiy at rest. Find the work done by this force on the body during first 2 seconds of its motion.
View Solution

