Using the Maxwell distribution function, calculate the mean velocity projection (vx) and the mean value of the modules of this projection <<|vx|>> if the mass of each molecule is equal to m and the gas temperature is T.
<vx>=0 bt symmetry
<|vx|>=∫∞−∞|vx|e−mv2x2kTdvx/∫∞0−mv2xe2kTdvx=∫∞0vx−mv2xe2kTdvx/∫∞0−mv2e2kTdvx
=√2kTm∫∞0ue−u2du/∫∞0e−u2du
=√2kTm∫∞012e−xdx/∫∞0e−xdx2√x
=√2kTmΓ(1)/Γ(12)=√2kTmπ.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy47videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects25videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The First Law Of Thermodynamics - Heat Capacity36videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
From the Maxwell distribution function frind <<v2x>>, the mean value of the squared vx projection of the molecular velocity in a gas at a temperature T. The mass of each molecule is equal to m.
View SolutionMaking use of the Maxwell distribution function, find <<1/v>>, the mean value of the reciprocal of the velocity of molecules in an ideal at a temperature T, it the mass of eacd molecule is equal to m. Compare the value obtained with the reciprocal of the mean velocity.
View SolutionMaking use of the Maxwell distribution function, calculate the number v of gas molecules reaching a unit area of a wall per unit time, if the concentration of molecules is equal to n, the temperature to T, and the mass of each molecule is m.
View SolutionUsing the Maxwell distribution function, determine the pressure exterted by gas on a wall, if the gas temperature is T and the concentration of molecules is n.
View SolutionFind the fraction of molecules whose velocity projections on the x axis fall within the inerval from vx to vx+dvx, while the moduli of perpendicular velocity components fall within the inerval from v⊥ to v⊥+dv⊥. The mass of each molecule is m, and the temperature is T.
View SolutionIn the case of gaseous nitrogen find :
(a) the temperature at which the velocities of the molecules v1=300m/s and v2=600m/s are associated with equal values of the Maxwell distribution friction F(v) ,
(b) the velocity of the molecules v at which the value of the Maxwell distribution function F(v) for the temperature T0 will be the same as that for the temperature η times higher.View SolutionFor the following distribution function F (X) of a r.v. X
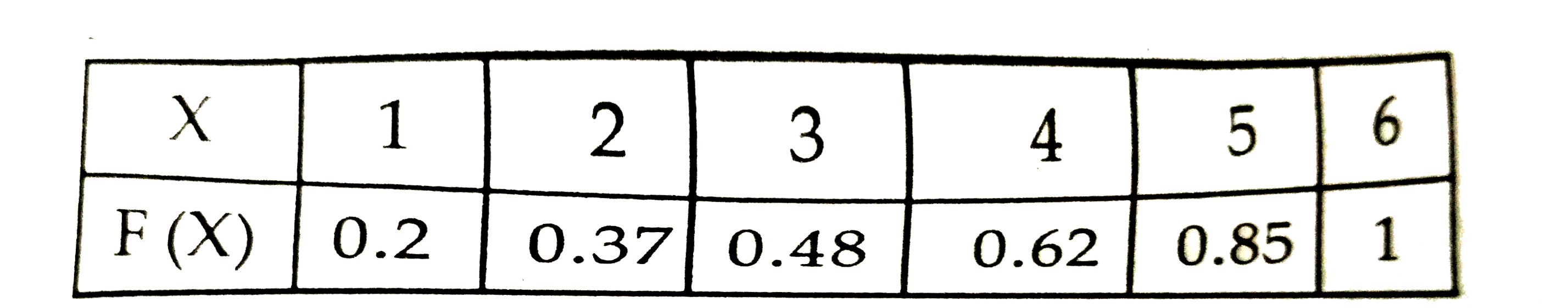
P(3<X≤5)=View SolutionAt what temperature of a gas will the number of molecules, whose velocities fall within the given interval from v to v+dv, be the greatest ? The mass of each molecule is equal to m.
View SolutionAt the moment t=0 a point starts oscillating along the x axis according to the laswx=asinωtt. Find:
(a) the mean value of its velocity vector projection (:vx:),
(b) the modulus of the mean velocity vector |(:v:)|,
(c) the mean value of the velocity modulus (:v:) averaged over 3/8 of the period after the start.View SolutionFor two gases, A and B with molecular weights MA and MB. It is observed that at a certain temperature. T, the mean velocity of A is equal to the root mean square velocity of B. thus the mean velocity of A can be made equal to the mean velocity of B, if:
View Solution

