(0,0) is the centre of the circle passing through the vertices of an equilateral triangle. If the length of the median of the triangle is 9 units then equation of the circle is
Step by step video & image solution for (0,0) is the centre of the circle passing through the vertices of an equilateral triangle. If the length of the median of the triangle is 9 units then equation of the circle is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The equation of the circle with origin as centre passing the vertices of an equilateral triangle whose median is of length 3a is
Ax2+y2=9a2Bx2+y2=16a2Cx2+y2=a2Dnone of the aboveThe equation of the circle with origin as centre passing the vertices of an equilateral triangle whose median is of length 3a is
Ax2+y2=9a2Bx2+y2=16a2Cx2+y2=a2Dnone of the aboveThe equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a, is
Ax2+y2=9a2Bx2+y2=16a2Cx2+y2=4a2Dx2+y2=a2
The radius of the circle passing through the vertices of the triangle ABC, is
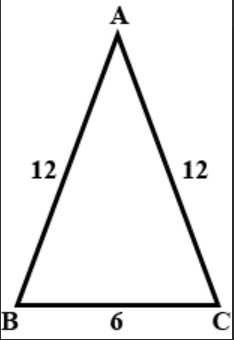
View SolutionThe radius of the circle passing through the vertices of the triangle ABC, is
View SolutionOrigin is the centre of a circle passing through the vertices of an equilateral triangie whose median is of length 3a then the equation of the circle is
View SolutionThe equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3 a is
View SolutionThe equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
View Solution
