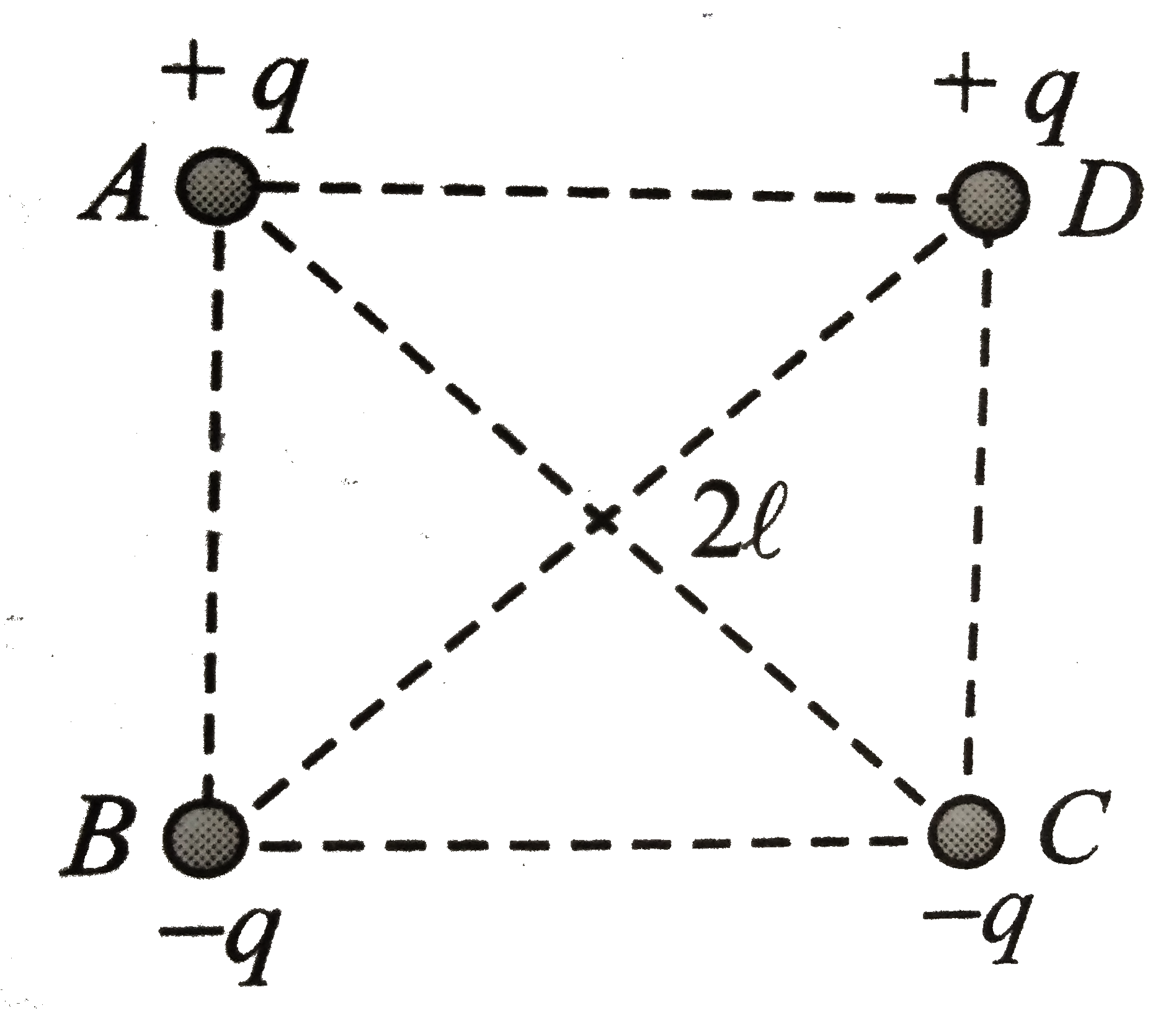
Point charge q and −q are located at the vertices of a square with diagonals 2l as shown in Fig. Find the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of the square at a distnace x from its centre.
To find the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of a square with charges q and −q at the vertices, we can follow these steps:
Step 1: Understand the configuration
We have a square with vertices A, B, C, and D. The charges are placed as follows:
- Charge +q at vertex A
- Charge −q at vertex B
- Charge −q at vertex C
- Charge +q at vertex D
The length of the diagonal of the square is 2l, which means the side length s of the square can be calculated using the relation s=2l√2=l√2.
Step 2: Identify the point of interest
We need to find the electric field at a point P that is located symmetrically with respect to the vertices of the square at a distance x from the center O of the square. The distance from the center O to any vertex (A, B, C, or D) is l.
Step 3: Calculate the distance from point P to each vertex
Using the Pythagorean theorem, the distance r from point P to any vertex (say vertex A) can be calculated as:
r=√x2+l2
Step 4: Calculate the electric field due to each charge
The electric field E due to a point charge Q at a distance r is given by:
E=14πϵ0⋅Qr2
For charge +q at A:
EA=14πϵ0⋅q(x2+l2)
For charge −q at B:
EB=−14πϵ0⋅q(x2+l2)
For charge −q at C:
EC=−14πϵ0⋅q(x2+l2)
For charge +q at D:
ED=14πϵ0⋅q(x2+l2)
Step 5: Determine the resultant electric field
The electric fields due to charges at A and D will point away from the charges (upwards), while the electric fields due to charges at B and C will point towards the charges (downwards). Since the magnitudes of the electric fields due to the charges at A and D are equal to those at B and C, the vertical components will cancel out.
The resultant electric field Enet at point P will be the vector sum of the electric fields due to the charges:
Enet=EA+EB+EC+ED=0
Step 6: Final expression for the electric field
Since the contributions from opposite charges cancel each other out, the net electric field at point P is:
Enet=0
Conclusion
The magnitude of the electric field strength at point P, located symmetrically with respect to the vertices of the square, is zero.
---
We have a square with vertices A, B, C, and D. The charges are placed as follows:
- Charge +q at vertex A
- Charge −q at vertex B
- Charge −q at vertex C
- Charge +q at vertex D
We need to find the electric field at a point P that is located symmetrically with respect to the vertices of the square at a distance x from the center O of the square. The distance from the center O to any vertex (A, B, C, or D) is l.
Using the Pythagorean theorem, the distance r from point P to any vertex (say vertex A) can be calculated as:
r=√x2+l2
The electric field E due to a point charge Q at a distance r is given by:
E=14πϵ0⋅Qr2
EA=14πϵ0⋅q(x2+l2)
EB=−14πϵ0⋅q(x2+l2)
EC=−14πϵ0⋅q(x2+l2)
ED=14πϵ0⋅q(x2+l2)
The electric fields due to charges at A and D will point away from the charges (upwards), while the electric fields due to charges at B and C will point towards the charges (downwards). Since the magnitudes of the electric fields due to the charges at A and D are equal to those at B and C, the vertical components will cancel out.
Enet=EA+EB+EC+ED=0
Since the contributions from opposite charges cancel each other out, the net electric field at point P is:
Enet=0
The magnitude of the electric field strength at point P, located symmetrically with respect to the vertices of the square, is zero.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Point chages q and -q are located at the verticles of a squre with diagonals 2l as shown in fig. Evaluate the magnitude of the electric field strength at a point located symmetrically with respect to the vertices of the square at a distanc x from the center.
 View Solution
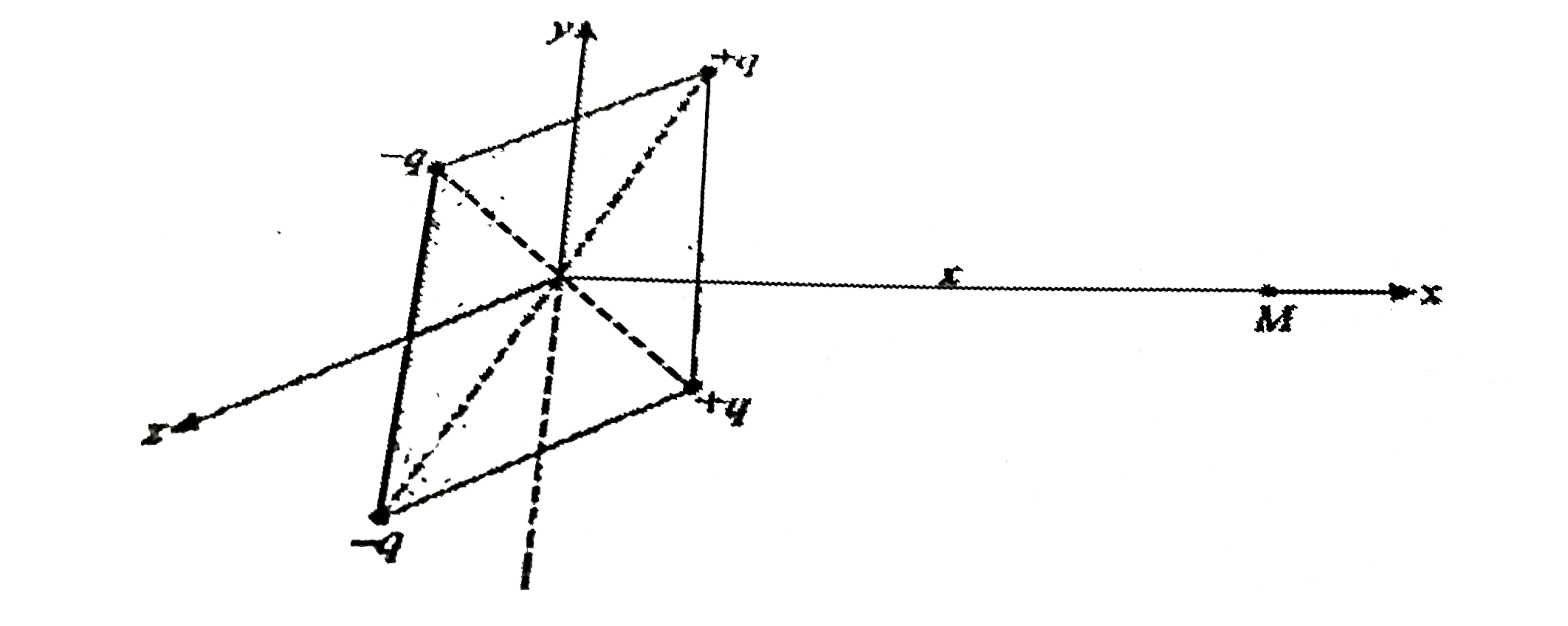
View SolutionPoint charges q and -q located at the vertices of a square with diagonals 2l as shown in figure. Find the magnitude of the electric field at a point located symmetrically with respect to the vertices of the square at a distance x from its centre. Consider x>>l0
[−ql√2πε0x3]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
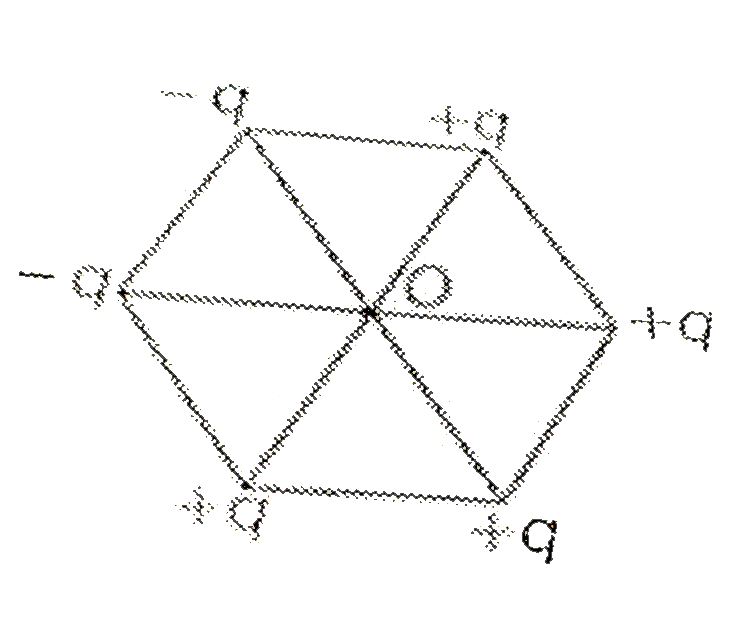
Find the magnitude of electric field at the centre of regular hexagon.Aq4πε0a2BzeroCq2πε0a2Dnone of these - Question 2 - Select One
Four point charge are placed at the corners of a square with diagonal 2a as shown. What is the total electric field at the center of the squre?
 Akq/a2 at an angle 45∘ above the +x-axisBkq/a2 at an angle 45∘ above the -x-axisC3kq/a2 at an angle 45∘ above the -x-axisD3kq/a2 at an angle 45∘ above the +x-axis
Akq/a2 at an angle 45∘ above the +x-axisBkq/a2 at an angle 45∘ above the -x-axisC3kq/a2 at an angle 45∘ above the -x-axisD3kq/a2 at an angle 45∘ above the +x-axis - Question 3 - Select One
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2
Four point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge QView SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the resultant electric force on a charge Q,View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .View SolutionElectric charges -q -q -q and 3q are placed at the corners of a square ABCD of length 1 as shown in figure.The magnitude of electric dipole moment of the system is
View Solution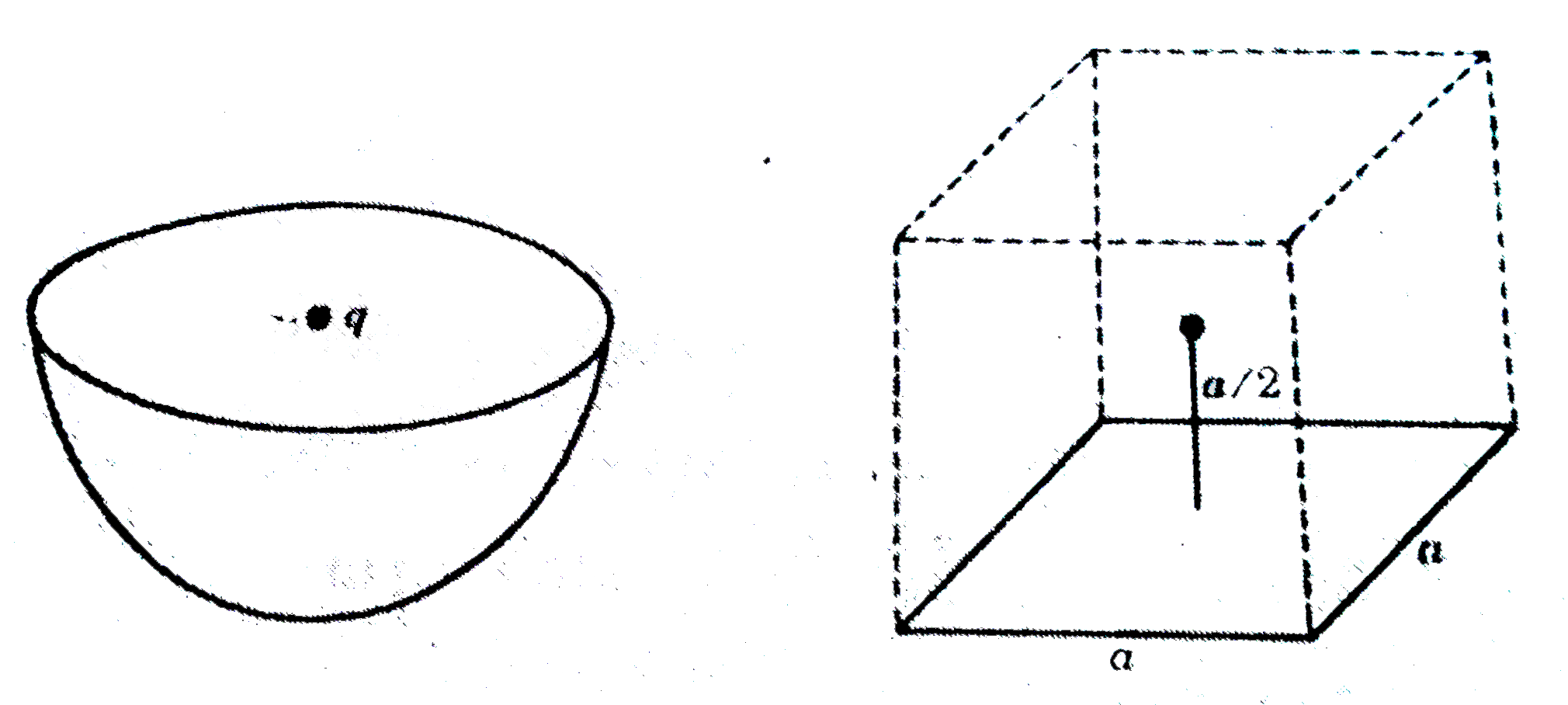
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.View Solution

