A whin wire ring of radius r carries charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance l from its centre. Investigate the obtained function at l>>r. Find the maximum strength magnitude and the corresponding distance l. Draw the appoximate polt of the function. E(l).
From the symmetry of the condition, it is clear that, the field along the normal will be zero
En=0 and E=E1
Now, dE1=dq4πε0(R2+l2)cosθ
But dq=q2πRdx and cosθ=1(R2+l2)1/2
Hence
E=∫dE1=∫2πR0ql2πR,dx4πε0(R2+l2)3/2
or E=14πε0ql(l2+R2)3/2
and for l>>R, the ring behaves like a point charge , reducing the field to the value,
E=14πε0ql2

For Emax, we should have dEdl=0
So, (l2+R2)3/2−32l(l2+R2)1/22l=0 or t2+R2−3l2=0
Thus l=R√2 and Emax=q6√3πε0R2
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
A thin half ring of radius R=20cm is uniformly charged with a total charge q=0.70nC.Find the magnitude of the electric field strength at the curvaite centre of this half-ring.
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32 - Question 2 - Select One
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A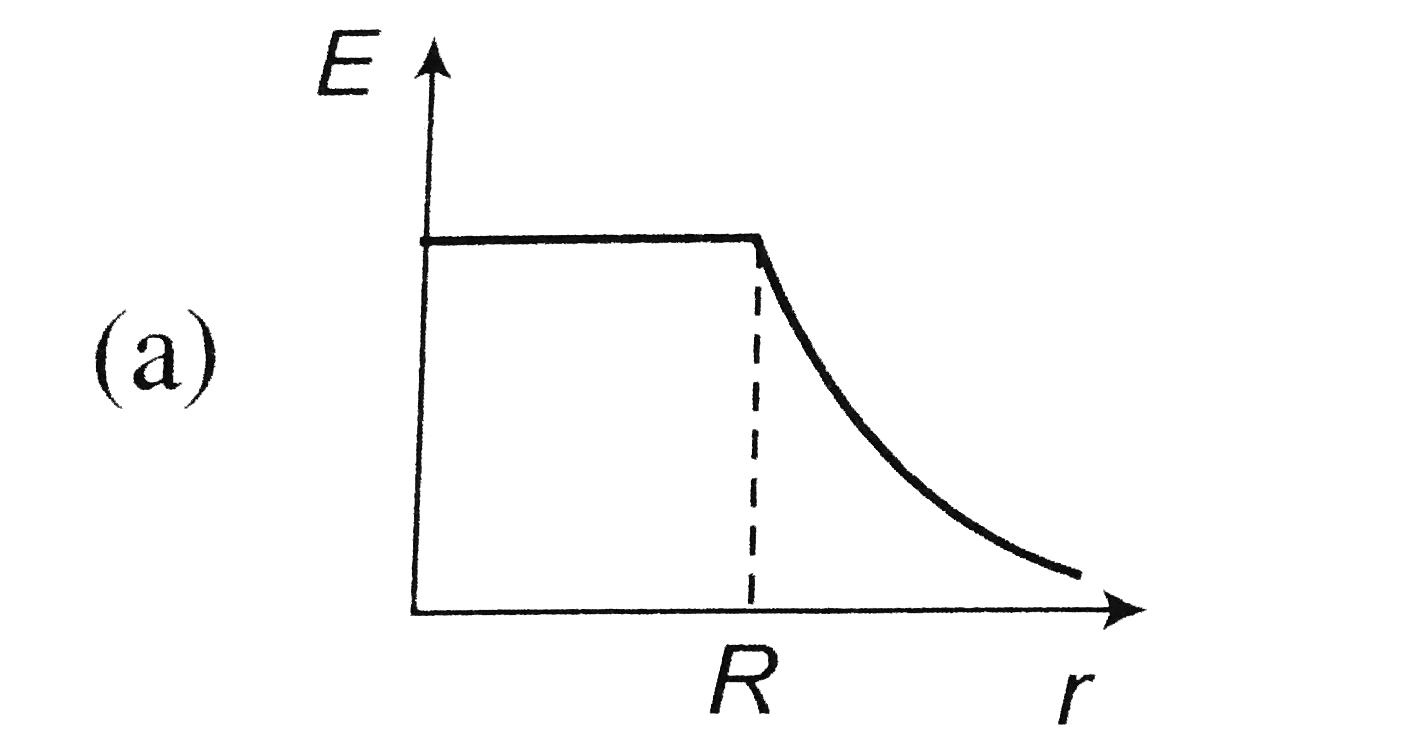 B
B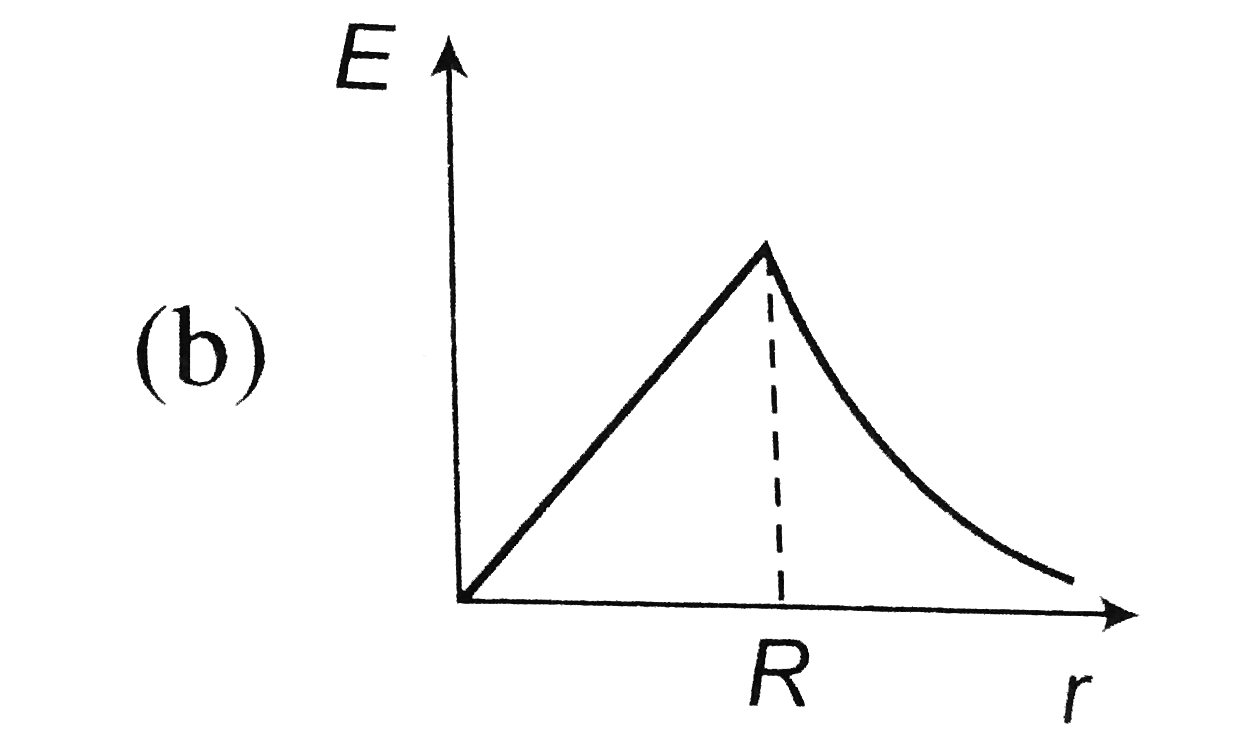 C
C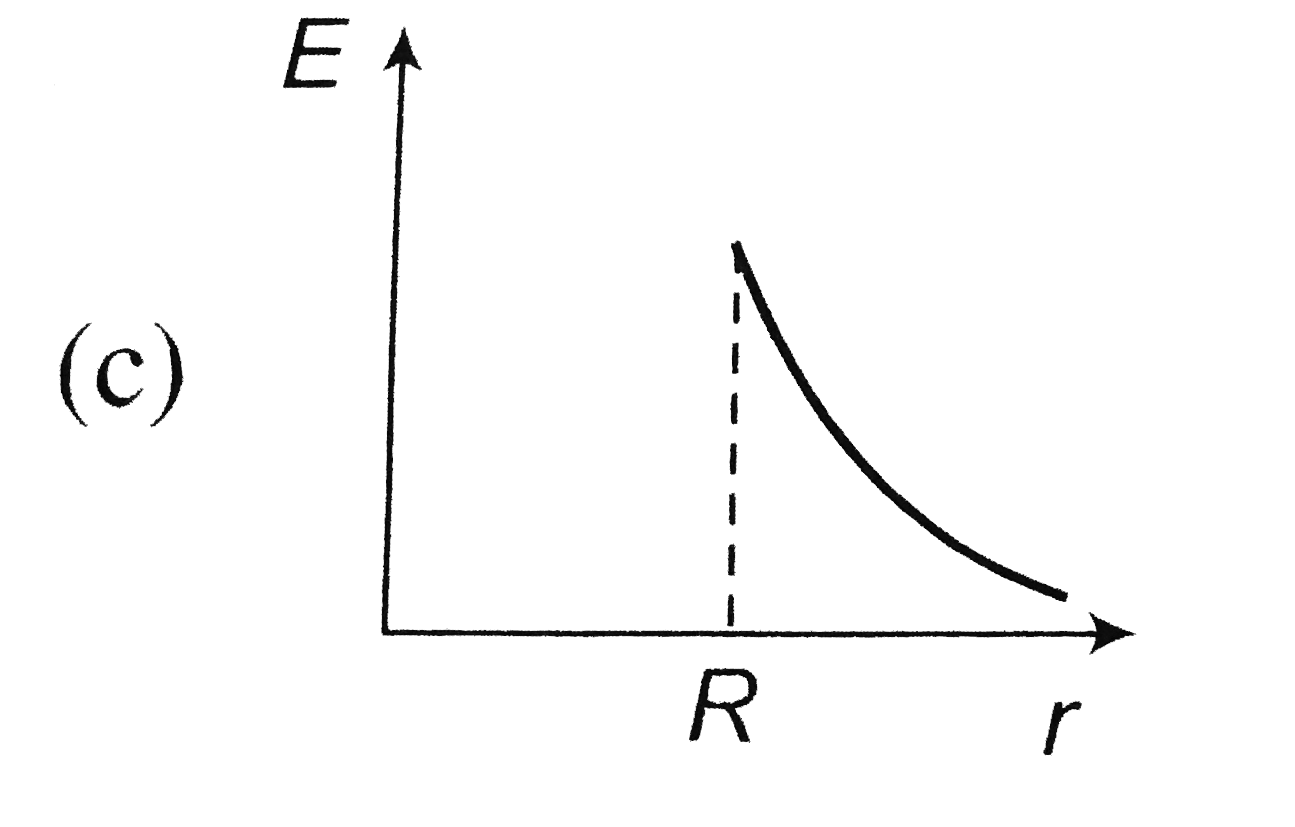 D
D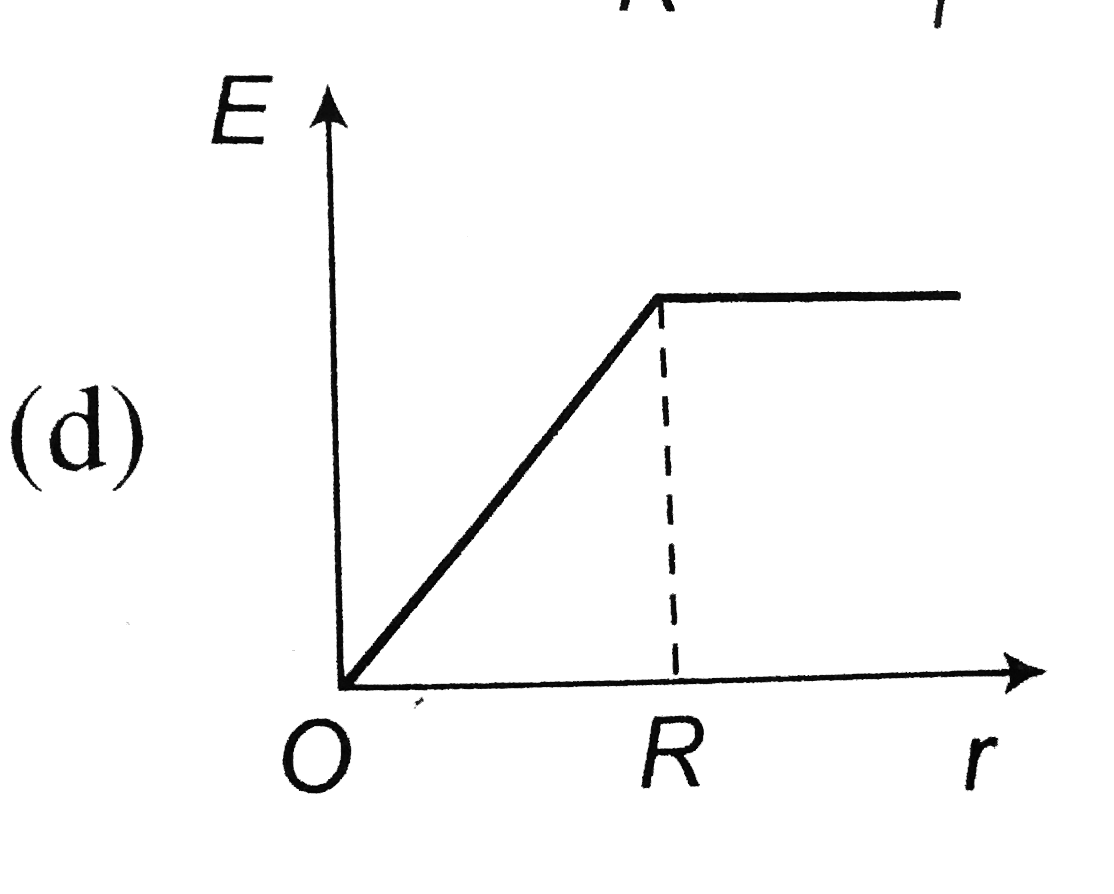
- Question 3 - Select One
A non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=R
A very thin round plate of radius R carrying a uniform surface charge density σ is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l→0 and l>>R.
View SolutionConsider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionFor a uniformly charged ring of radius R, the electric field on its exis has the largest magnitude at a distance h from its centre. Then value of h is :
View SolutionA thin wire ring of radius r has an electric charge q. What is the tension of the wire if a point charge q0 is placed at the ring's centre?
View Solution

