Each of the two long parallel threads carries a uniform charge λ per unit length. The threads are separated by a distance l. Find the maximum magnitude of the electric firld strength in the symmetry plane of theis system located between the threads.
The field at P due to the threads at A and B are both of magnitude λ2πε0(x2+l2/4)1/2 and directed along AP and BP. The resulatant is along OP with
E=2λcosθ2πε0(π2+π1/2)1/2=λxπε0(x2+l2/4)
=λπε0[x+l24x−2.12√x.√x+l]
=λ4ε0[(√x−l2√x)2+l]
This is maximum when x=l/2, and then E=Emax=λπε0l

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Two point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View SolutionA very long straight uniformly charged thread carries a charge λ per unit length. Find the magnitude and direaction of the electric field strength at point which is at a distance y from the thread and lies on the perpendicular passing through one of the thread's ends.
View Solution
Knowledge Check
Each of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
Aμ0iπRBzeroCμ0iπ√R2−l2Dμ0iπR√1−l2R2A long strikes with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
Aλaε0B√λaε0C6λa2ε0D√3λaε0Two thin long parallel wires separated by a distance 'd' are carrying same current I. The magnitude of the force per unit length exerted by one wire on the other is
Aμ0I2d2Bμ0I22πdCμ0I2πdDμ0I2πd2
A thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
 ,
, 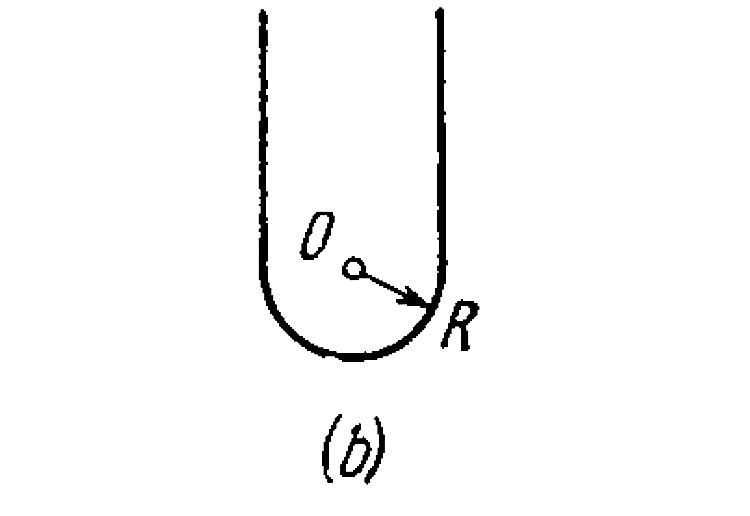
View SolutionTwo this parallel threads carry a uniform charge with linear densities lamnda and −λ . The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r>>l at the angle θ to the vector 1 (fig).
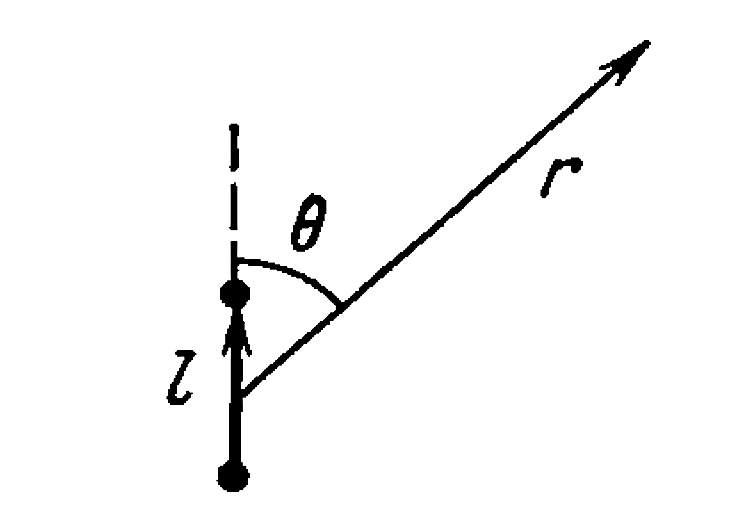
View SolutionTwo long straight parallel wires carry charges λ1andlamba2 per unit length. The distance between them is d. Calculate the magnitude of force externed on the length of one due to charge on the other.
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo thin long paralel wires separated by a distance b are carrying a current 1 A each. The magnitude of the force per unit length exerted by one wire on the other is
View Solution
