An infineltly long cylindrical surface density σ=σ0cosφ. Where φ is the polar angle of the cylindrical coordinate system whose z axis coincides with the axis of the given surface. Find the magnitude and direction of the electric fiels strength vector on the z axis.
Take a section fo the cylinder perpendicualr to its axis through the point where the electric field is to be calculated. (All points on axis are equivalent.) Consider an element S with azimuthal angle φ. The length of the element is Rdφ,R being teh radius of cross section of the cylinder. The element iteself is a section of an infinite strip. The electric field O due to this strip is
σ0cosφ(Rdφ)2πε0R along SO
This can be resolved into
σ0cosφdφ2πε0{cosφ along OX towards Osinφ along YO
On intergation the component along YO vanishes. What remain is
∫2π0σ0cos2φdφ2πε0=σ02ε0 alonng XO i.e, along the direction φ=π.

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
When an uncharged conducting ball of radius R is placed in an external uniform electric field, a surface charge densityh σ=σ0cosθ is induced on the ball's surface charge (here σ0 is a constant, θ is a polar angle). Find the magnitude of the resultant electric force acting on an induced charge of the same sign.
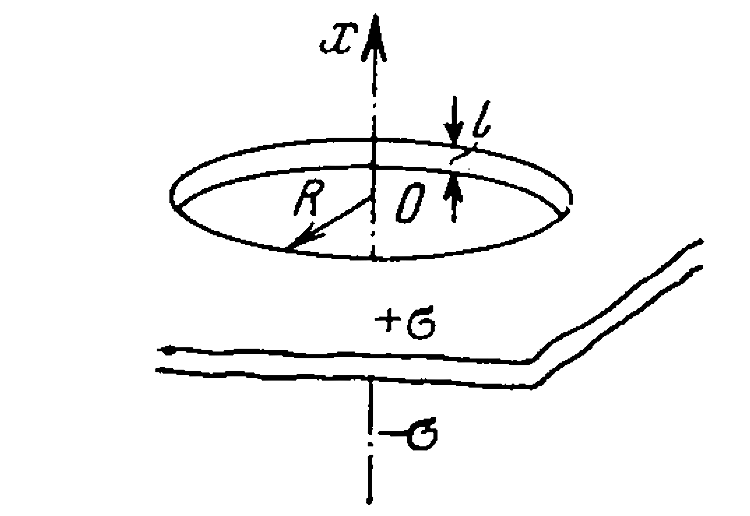
View SolutionTwo infinite planes sepated by a distance l carrying a uniform surface charge of densities σ and −σ. The planes have round coaxial holes of radius R, with l<<R. Taking the origin O and the x cordinates axis as shown in the figure, find the potentail of the electric field and the projection of its strength vector Ex on the area of the system as functions of the x cordiante. Draw the appoximate plot φ(x).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)
A thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius r and length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionIn a long insulating cylinder of radius R a cylindrical tunnel of radius a located at a distance b from the axis of the cylinder as shown in the figure. R R b - The solid part of the cylinder has a uniform volume charge density P. Find the magnitude and direction of the electric field inside the tunnel.
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.View SolutionState Gauss' law in electrostatic.. A thin straight infinitely long conducting wire of linear charge density λ is enclosed by a cylinder surface of radius 'r' and length ''l' ,its axis coinciding with the length of the wire . Qbtain the expressionn for the electric field, indicating its direction at a point on the surface of the cylinder.
View SolutionA thin straight infinitely long conducting wire having charge density λ is enclosed by a cylinder surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionA long straight cylindrical region of radius a curries a current along its length. The current density (J) varies from the axis to the edge of the cylindrical region according to J=J0(1–ra) Where r is distance from the axis (0<r<a)
(a) Find the mean current density.
(b) Plot the variation of magnetic field (B) with distance r from the axis of the cylinder for 0<r<a.View Solutiona)State Gauss’s law in electrostatics. Show that with help of suitable figure that outward flux due to a point charge Q, in vacuum within gaussian surface, is independent of its size and shape.
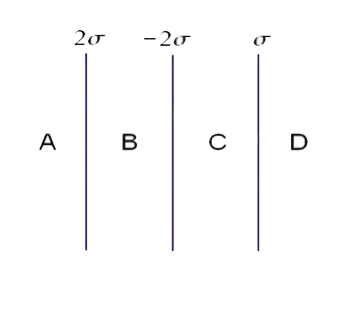
b) In the figure there are three infinite long thin sheets having surface charge density +2σ,−2σand+σ respectively. Give the magnitude and direction of electric field at a point to the left of sheet of charge density +2σ and to the right of sheet of charge density +σ
 View Solution
View Solution

