Find the potential at the edge of a thin disc of radius carrying the uniformly distributed charge with surface density .
By definition, the potentail in the case fo a surface charge distribution is defined by intergal , In order to simply intergation we shall choose the area element in the from of a part of the ring of radius width in (Fig). Then and . After subsituating these expressions into intergal
, we obtain the expression for for at the point :
We intergate bty parts,
denoting and ,
which gives after substuting the limits of interfation. As a result, we obtain

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One or More
A thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
AThe magnetic field intensity at the centre of the disc is μ0Qω3πRBThe magnetic field intensity at the centre of the disc is μ0Qω4RCThe magnetic moment of the disc is 5QωR216DThe magnetic moment of the disc is 3QωR24 - Question 2 - Select One
Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
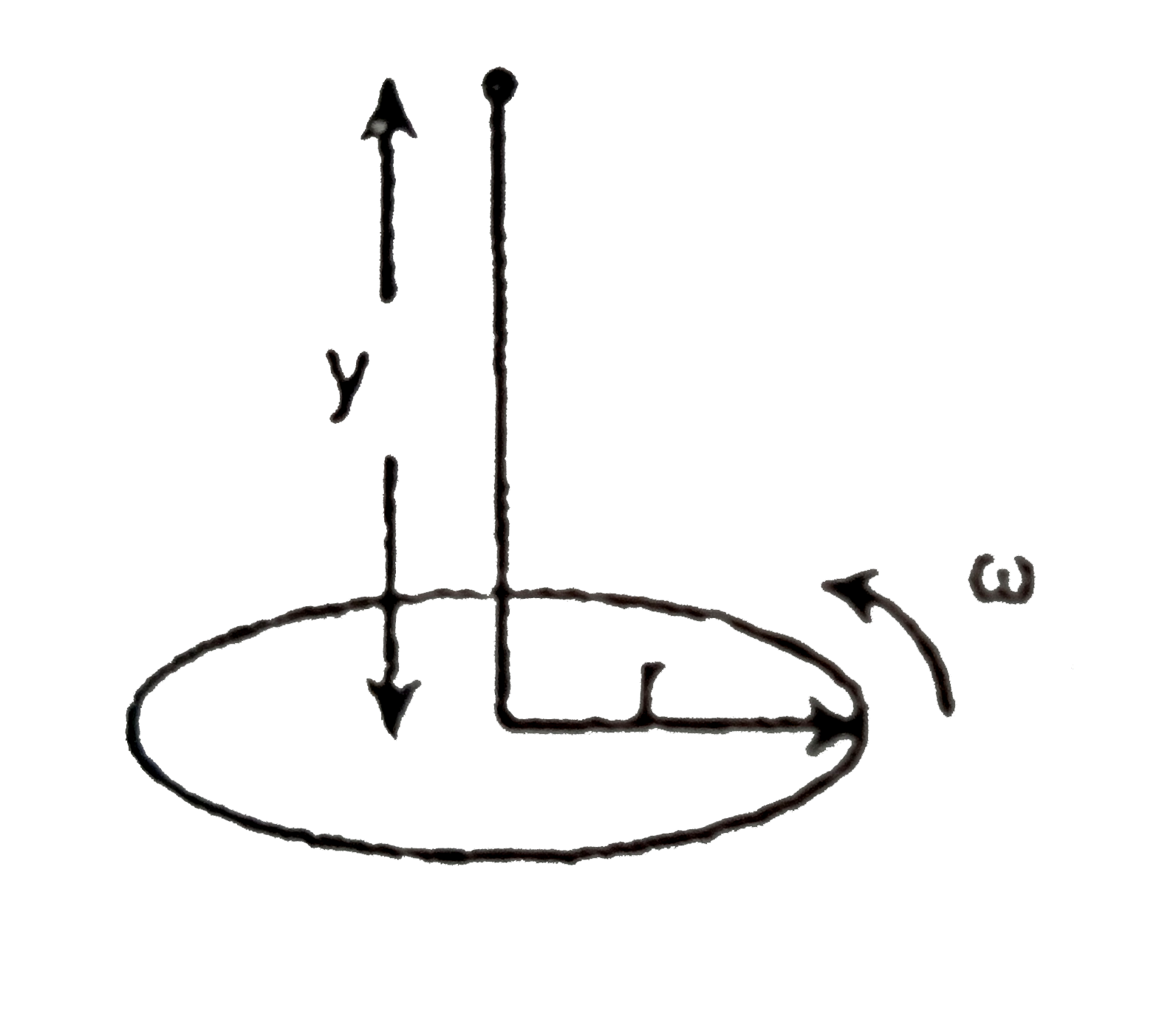 Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
The diagram shows a part of disc of radius R carrying uniformly distributed charge of density σ. Electric potential at the centre O of parent disc is
View SolutionRepeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionDerive the expression of electric field intensity at a point 'P' which is situated at a distance x on the axis of uniformly charges disc of radius R and surface charge density σ. Also, derive results for
(i) x>>R (ii) x<<RView SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density σ rotates about its axis with an angular velocity ω. Find :
(a) the magnetic induction at the centre of the disc,
(b) the magnetic moment of the disc.
( c) the ratio of magnetic moment and angular momentum of disc.View Solution

