Determine the potential at point 1 of the circuit shown in Fig., assuming the potential at the point O to be equal to zero.
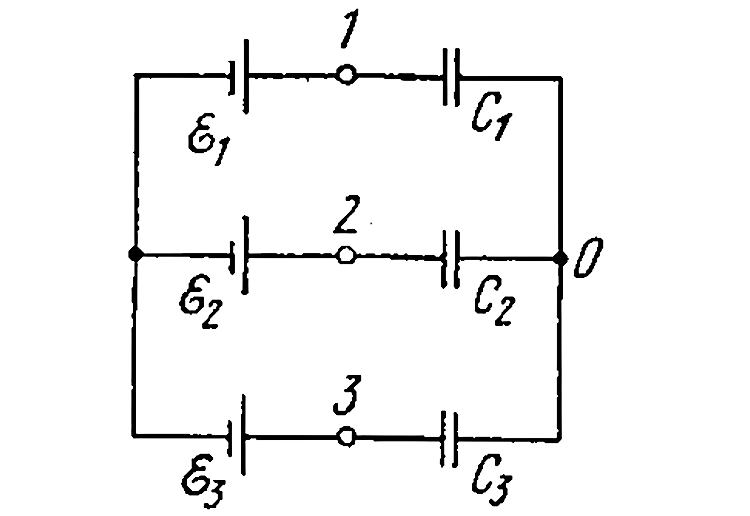
using the symmetry of the formula obtained, write the expressions for the potentials at points 2 and 3.
Video Solution
Text Solution
In the loop ABDEA, using −Δφ=0
−ξ3+q1C3+q1+q2C1+ξ1=0 ....(1)
similarly in the loop ODEF,O
q1+q2C1+ξ1−ξ2+q2C2=0 ....(2)
Solving Eqs. (1) and (2) we get,
q1+q2=ξ2C2−ξ1C2−ξ1C3+ξ3C3C3C1+C2C1+1
Now, φ1−φ0=φ1=−(q1−q2)C1, as (φ0=0)
=ξ1(C2+C3)−ξ0C2−ξ3C3C1+C2+C3
And using the symmetry, φ2=ξ2(C1+C3)−ξ1C1−ξ3C3C1+C2+C3
and φ3=ξ3(C1+C2)−ξ1C1−ξ2C2C1+C2+C3
The answers have wrong sign in the book.

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics69videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
The potential of the point O is
 . A3.5 VB6.5 VC3 VD6 V
. A3.5 VB6.5 VC3 VD6 V - Question 2 - Select One
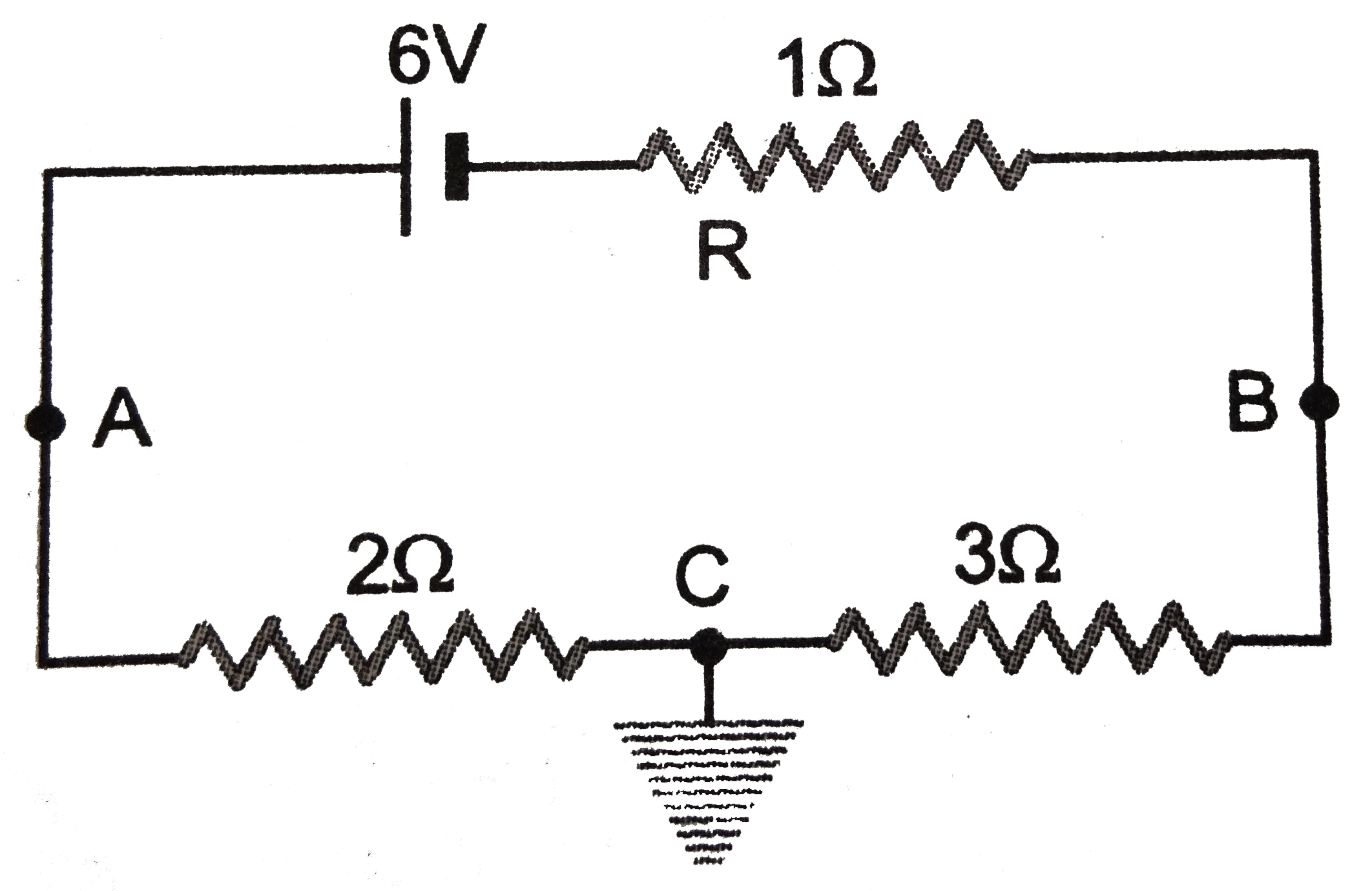
In the circuit shown, the point B is earthed. The potential at the point 'A' is
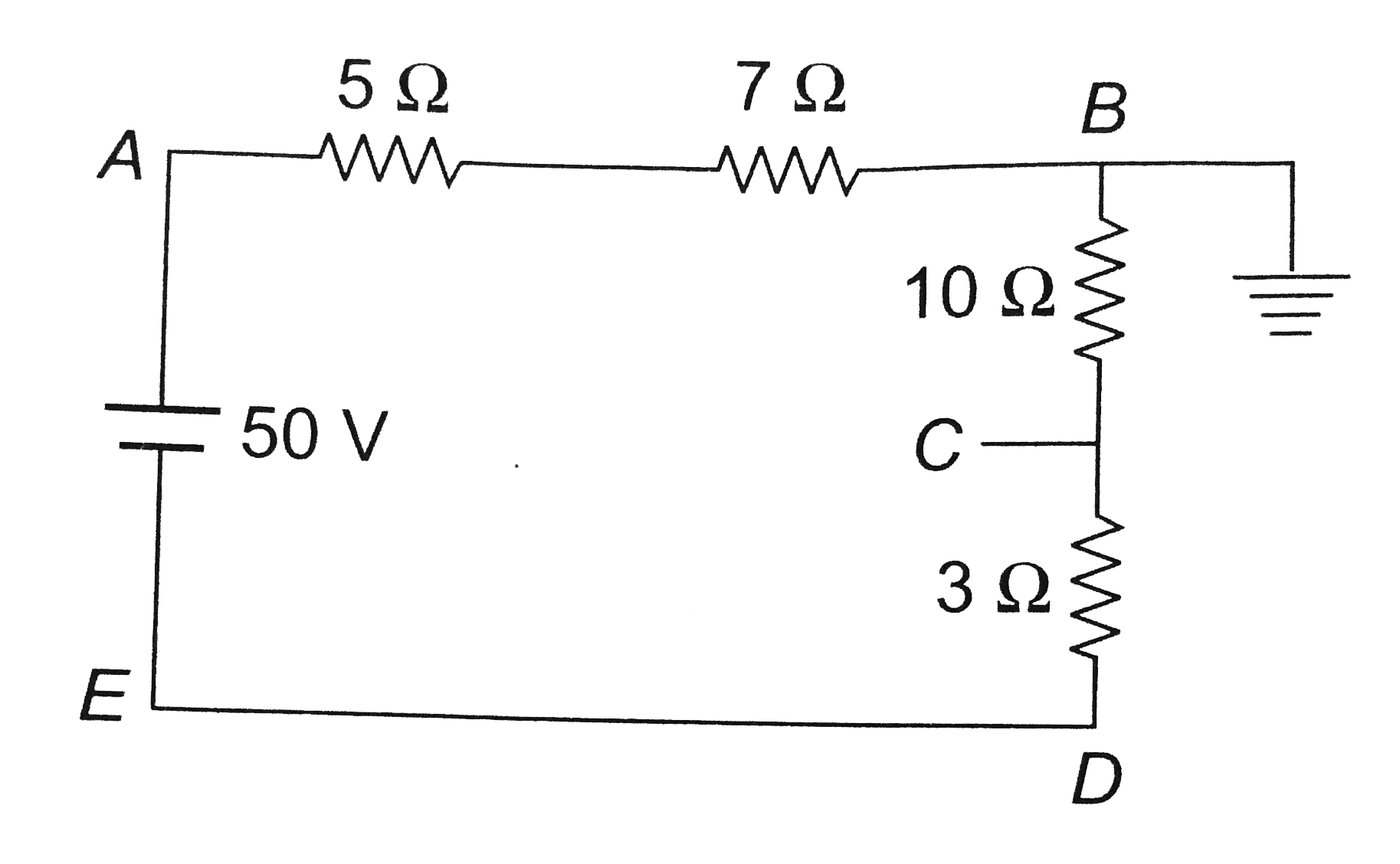 A14VB24VC26VD50V
A14VB24VC26VD50V - Question 3 - Select One
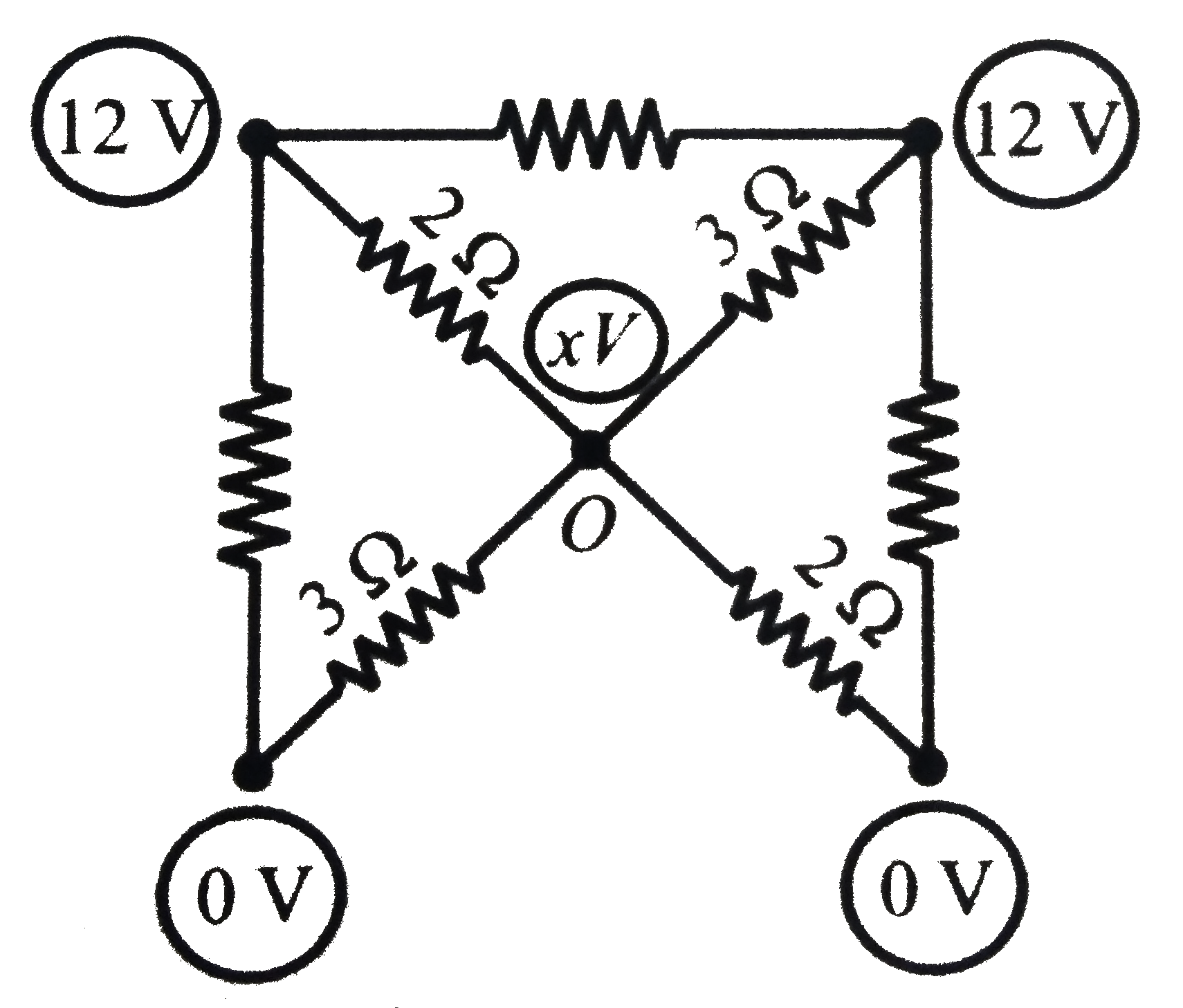
In the circuit shown if point O is earthed, the potential of point X is equal to
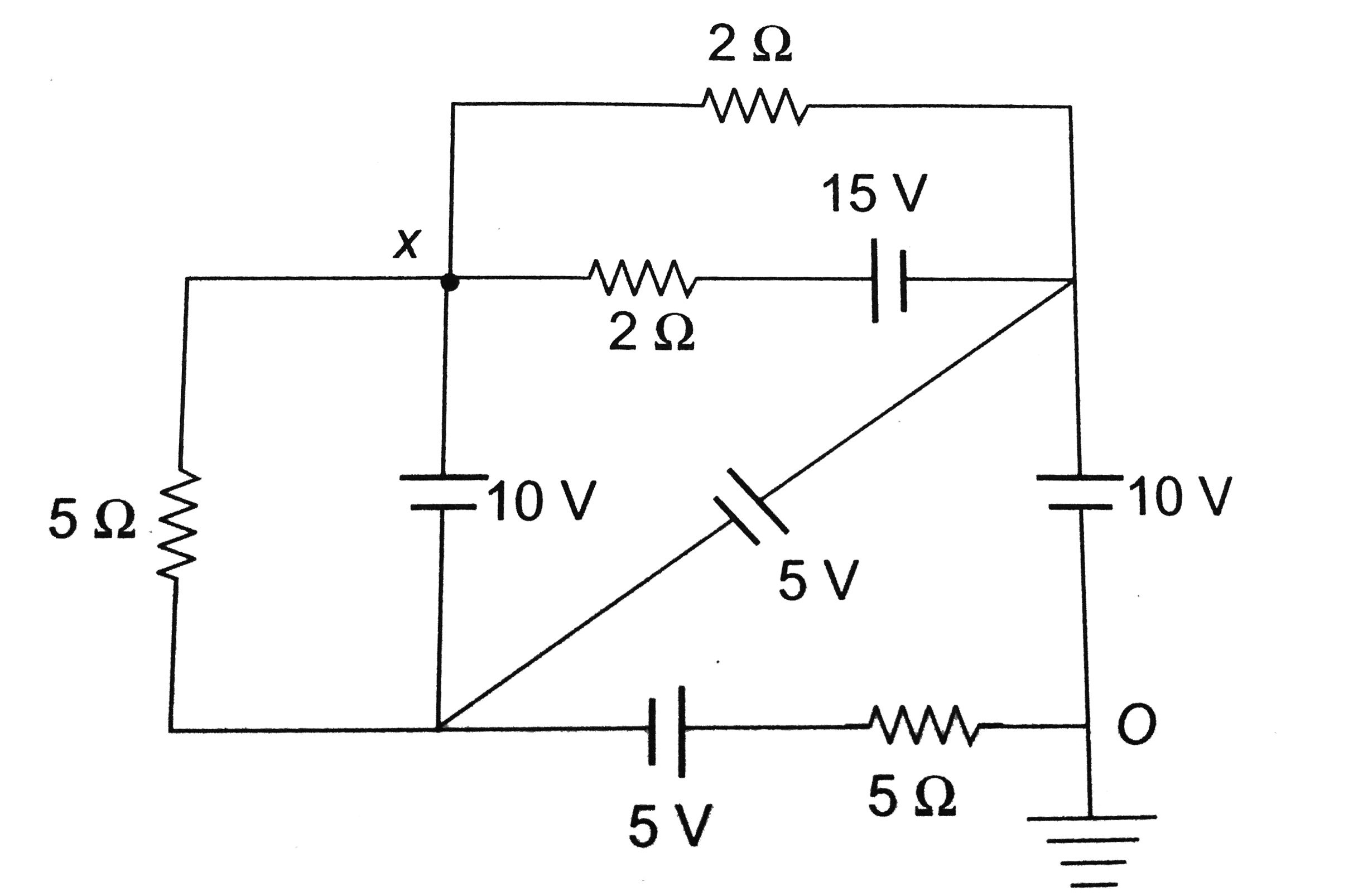 A10VB15VC25VD12.5V
A10VB15VC25VD12.5V
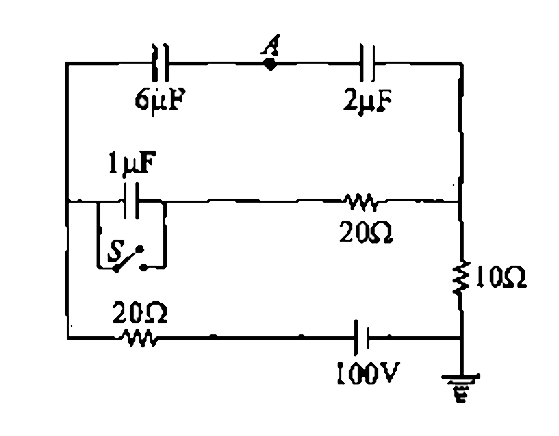
In a circuit shown in the figure, what is potential of point A?
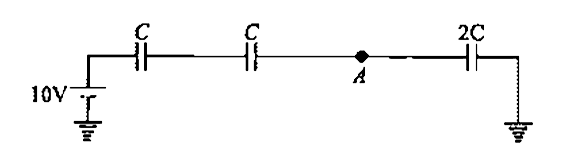 View Solution
View SolutionThe potnetial at point A, in the circuit, is (Point N is grounded, i.e. the potential of that point is zero.)
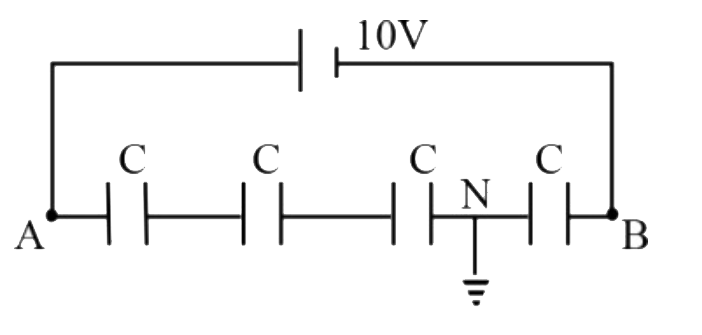 View Solution
View SolutionIn the given circuit, the potential of the point E is
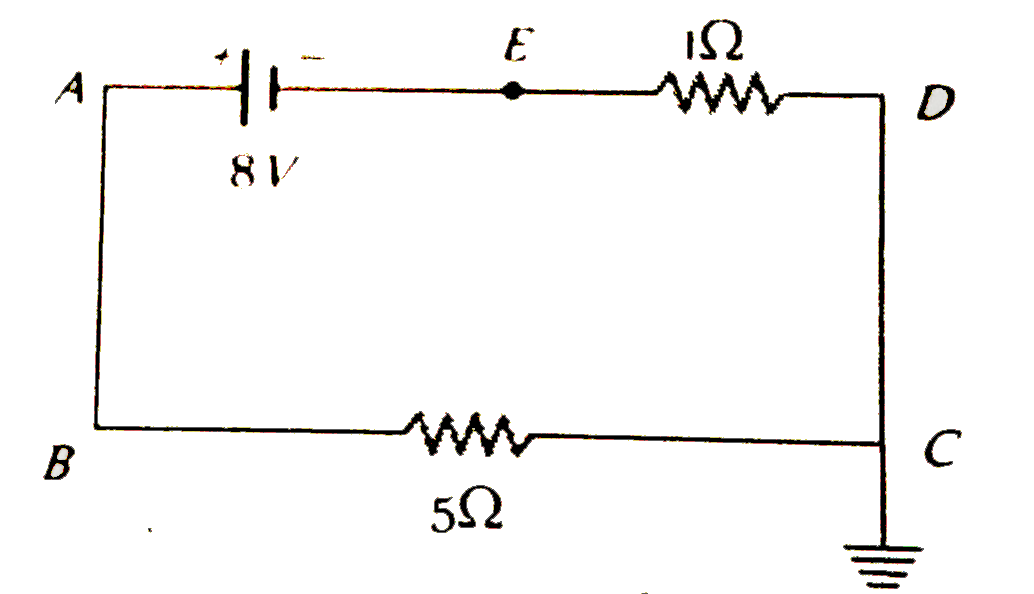 View Solution
View SolutionThe potential at point A in the circuit is - (N point is grounded. Grounding menas that potential of that point is zero.)
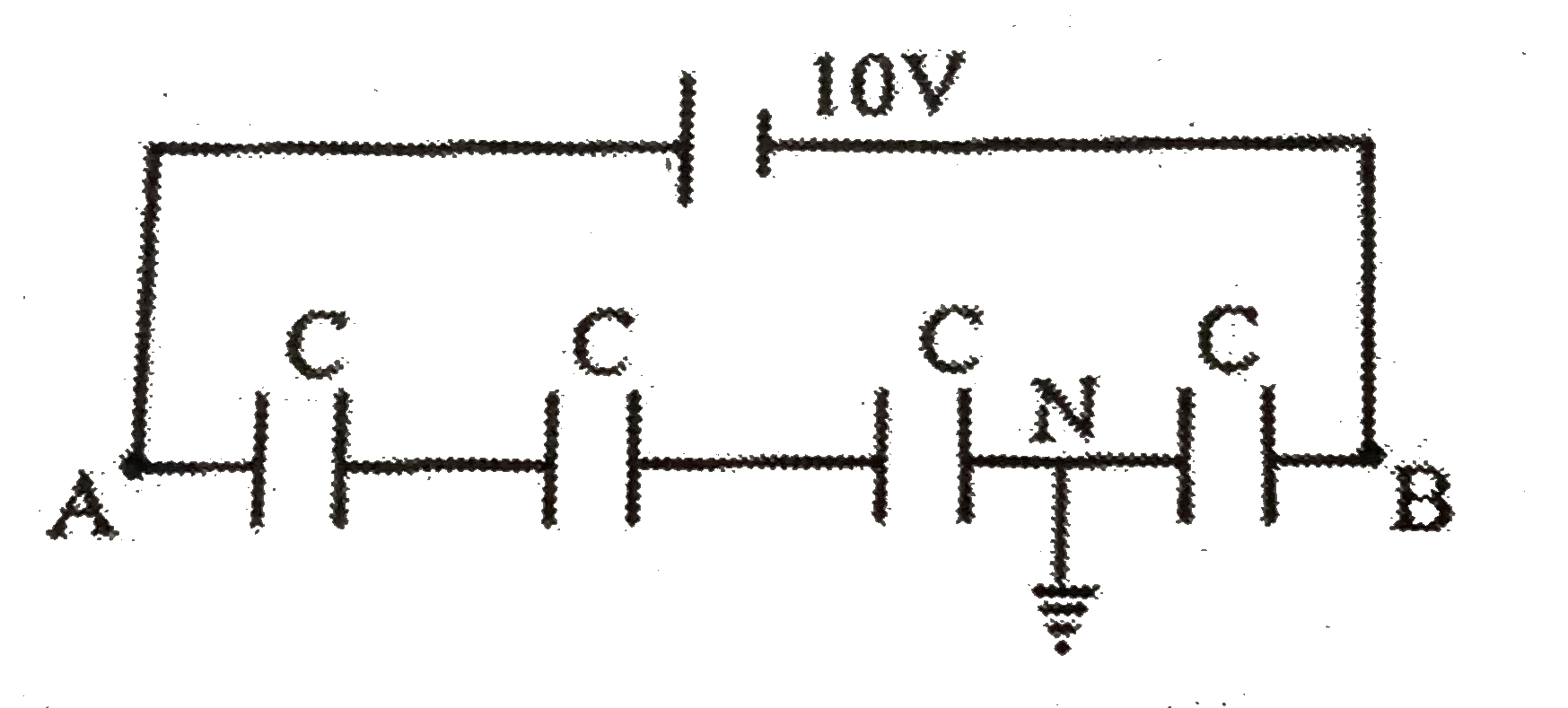 View Solution
View SolutionIn the circuit shown in the figure, if the potential at point A behind to be zero, the potential at point B is :
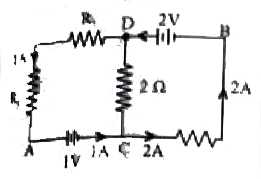 View Solution
View Solution