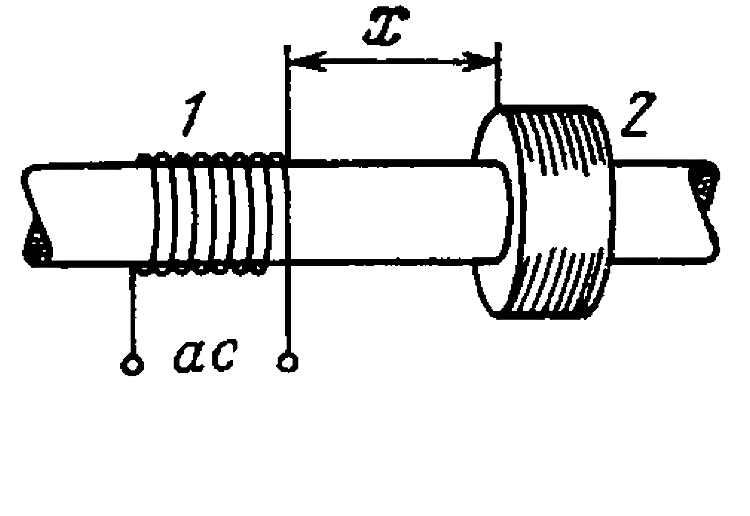
A wooden core $($ figure $)$ supports two coils $:$ coil $1$ with inductance $L_{1}$ and shor $-$ circuited coil 2 with active resistance $R$ and inductance $L_{2}$ . The mutual inductance of the coils depends on the distance $x$ between them according to the law $L_{12} (x)$ . Find the mean $($ averaged over time $)$ value of the interaction force between the coils when coil 1 carries an alternating current $I_{1} = I_{0} cos ω t$

Text Solution

Verified by Experts

We consider the force $- \to F_{12}$ that a circuit 1 exerts on another closed circuuit 2 $: -$
$- \to F_{12} = \oint I_{τ} d \to l_{2} \times - - \to B_{12}$
Here $- - \to B_{12} =$ magnetic field at the site of the current element $d \to l_{2}$ due to the current $I_{1}$ flowing in 1 .
$= \frac{μ_{0}}{4 π} \int \frac{I_{1} d \to l_{1} \times - \to r_{12}}{r_{12}^{3}}$
where $- \to r_{12} = \to r_{2} - \to r_{1} =$ vector, current element $d \to l_{1}$ to the current element $d \to l_{2}$
Now
$- \to F_{12} = \frac{μ_{0}}{4 π} \int \int I_{1} I_{2} \frac{d \to l_{2} \times (d \to l_{1} \times - \to r_{12})}{r_{12}^{3}} = \frac{μ_{0}}{4 π} \int \int I_{1} I_{2} \frac{d \to l_{2} (d \to l_{2} . - \to r_{12}) - (d \to l_{1} . d \to l_{2}) - \to r_{12}}{r_{12}^{3}}$
In the first term, we carry out the integration over $d \to l_{τ}$ first. Then
$\int \int \frac{d \to l_{1} (d \to l_{2} . - \to r_{12})}{r_{12}^{3}} = \int d \to l_{2} \oint \frac{d \to l_{2} . - \to r_{12}}{r_{12}^{3}} = - \int d \to l_{1} \oint d \to l_{2} . \nabla_{2} \frac{1}{r_{12}} = 0$
because $\oint d l_{2} . \nabla_{2} \frac{1}{r_{12}} = \int d \to S_{2} c u r l (\nabla \frac{1}{r_{12}}) = 0$
Thus $F_{12} = - \frac{μ_{0}}{4 π} \int \int I_{1} I_{2} d \to l_{1} . d \to l_{2} \frac{- \to r_{12}}{r_{12}^{3}}$
The integral involved will depend on the vector $\to a$ that defines the separation of the $($ suitably chosen $)$ centre of the coils . Let $C_{1}$ and $C_{2}$ be the centres of the two coil suitably defined.
Write
$- \to r_{12} = \to r_{2} - \to r_{1} = \to ρ_{2} - \to ρ_{1} + \to a$
where $\to ρ_{1} (\to p_{2})$ is the distance of $d \to l_{1} (d \to l_{2})$ from $C_{1} (C_{2})$ and $\to a$ stands for the vector $C_{1} - \to C_{2}$ .
Then $\frac{- \to r_{12}}{r_{12}^{3}} = - - - \to \nabla_{\to a} \frac{1}{r_{12}}$
and $- \to F_{12} = {- -- \to grad}_{a} ⎡ ⎢ ⎣ I_{1} I_{2} \frac{μ_{0}}{4 π} \int \int \frac{d \to l_{1} . d \to l_{2}}{r_{12}} ⎤ ⎥ ⎦$
The bracket defines the mutual inductance $L_{12}$ . Thus noting the definition of $x$
$< F_{x} > = \frac{δ L_{12}}{δ x} < I_{1} I_{2} >$
where $< >$ denotes time average. Now
$I_{1} = I_{2} cos ω t =$ Real part of $I_{0} e^{i ω t}$ ltbr> The current in coil 2 satisfies $R I_{2} + L_{2} \frac{d I_{2}}{d t} = - L_{12} \frac{d I_{1}}{d t}$
or $I_{2} = \frac{- i ω L_{12}}{R + i ω L_{2}} I_{0} e^{i ω t}$ ( in the complex case)
taking the real part
$I_{2} = - \frac{ω L_{12} I_{0}}{R^{2} + ω^{2} L_{2}^{2}} (ω L_{2} cos ω t - R sin ω t) = - \frac{ω L_{12}}{\sqrt{R^{2} + ω^{2} L_{2}^{2}}} I_{0} cos (cos ω t + φ)$
Where $tan φ = \frac{R}{ω L_{2}}$ . Taking time average, we get
$< F_{x} > = \frac{δ L_{12}}{δ x} I_{0} \frac{ω L_{12} I_{0}}{\sqrt{R^{2} + ω^{2} L_{2}^{2}}} . \frac{1}{2} cos φ = \frac{ω^{2} L_{2} L_{12} I_{0}^{2}}{2 (R^{2} + ω^{2} L_{2}^{2})} \frac{δ L_{12}}{δ x}$
The repulsive nature of the force is also consistent with Lenz's law, assuming, of comse, that $L_{12}$ decreases with $x$ .

Updated on:21/07/2023

The mutual inductance of coil does not depend on
Anumber of turns of the coil
Bgeometrical properties of the coil
Cpermebility of the medium
Dall of the above
Mutual inductance of two coils depends on their self inductance $L_{1}$ and $L_{2}$ as :
A $M_{12} = L_{1} / L_{2}$
B $M_{12} = L_{2} / L_{1}$
C $M_{12} = \sqrt{L_{1} L_{2}}$
D $M_{12} = \sqrt{L_{1} / L_{2}}$
The mutual inductance $M_{12}$ of coil 1 with respect to coil 2
Aincreases when they are brought nearer
Bdepends on the current passing through the coils
Cincreases when one of them is rotated about an axis
Dis the same as $M_{21}$ coil 2 with respect to coil 1