Suppose F' and F' are the front and rear focqal points of an optical system, and H' and H' are its front and rear principle points. By means of plotting relative positions of the points S,F,F',H, and H':
(a) FSHH'F', (b) HSF'FH', (c) H'S'FH, (d) F'H'SHF.
Here we do not assume that the media on the two sides of the system are the same.




Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light60videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
An optical system is located in air. Let OO' be its optical axis, F' and F' are the front and rear focal points, H and H' are the front and rear principle planes, P and P' are the conjugate points. By means of plotting find:
(a) the position F' and H' (Fig.),
(b) the position of the point S' conjugate to the point S (Fig.),
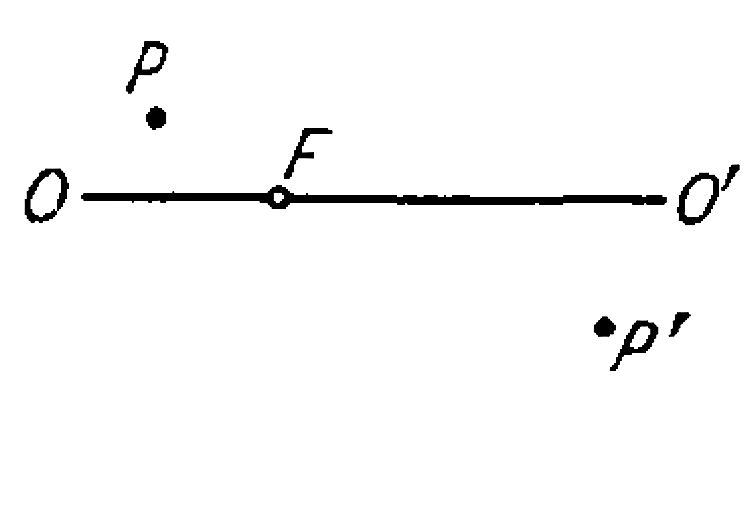
(c) the positions F,F', and H' (Fig. where the path of the ray of light is shown before and after pasing through the system).View SolutionLet the tangent to the graph of y=f(x) at the point x=a be parallel to the x-axis and let f'(a−h)>0andf(a+h)<0, where h is a very small positive number.Then, the ordinate of the points is
View Solution
Knowledge Check
- Question 1 - Select One
In a bicycle the radius of rear wheel is twice the radius of front wheel. If vF and vr are the speeds of top most points of front and rear wheels respectively, then :
Avr=2vFBvF=2vrCvF=vrDvF>vr - Question 2 - Select One
F.H. Buchanan, a traveller describes the life of pastoral community of
AThe Gollas of MysoreBThe Gaddi Shepherds of Himachal PradeshCThe Banjaras of Andhra PradeshDAll the above - Question 3 - Select One
H.C.F of 87 and 145 is
A870B1305C29D1740
Calculate the theoretical value of bond length in H−F , if fH and rF are −0.37Å respectively. Electronegativites of F and H are 4.0 and 2.1 respectively .
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionThe increasing order of the strength of hydrogen bond in the following mentioned linkages is :
(i)O-H-S (ii)S-H-O (iii)F-H-F (iv)F-H-OView Solution

