A plane monochromatic wave of natural light with intensity I0 falls normally on an opaque screen with round hole corresponding to the first Fresnel zone for the observation point P. Find the intensity of light at the point P after the hole was converd with two identical Polaroids whose principle directions are mutually perpendicular and the boundary beween them passes
(a) along the diameter of the hole,
(b) along the circumference of the circle limiting the first half of the fresnel zone.
Assume first that there is no polaroid and the amplitude due to the entire hole which extends over the first Fresnel zone is A1
then, we know, as equal, I0=A214,
When the polaroid is introduced as shown above, eaxh half transits only the corresponding polarized light. if the full hole were coveres by one polaroid the ampliyude transmitted will be (A1/√2).
Therefore the amplitude transmitted in the present case will be A12√2 through either half.
Since these transmitted waves are polarized in mutually perpendicualr planes, the total intensity will be
(A12√2)2+A1(2√2)2=A214=I0.
(b) We interpert the problem to mean that the two polaroid pieces are separated along the circulference of the circle limiting the first half of the Fresnel zone. (This however is inconsistent with the polaroids being identical in shape, however no other interpretaion makes sense.)
From (5.103) and the previous problem we see that the amplitudes of the waves transmitted through the two parts is
A12√2(1+i)and A12√2(1−i)
and the intensity is
∣∣
∣∣A212√2(1+i)∣∣
∣∣2+∣∣∣A12√2(1−i)∣∣∣2
=A212=2I0

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
A plane monochromatic light wave with intensity I0 falls normally on an opaque disc closing the first Fresnel zone for the observation point P. What did the intensity of light I at the point P become equal to after
(a) half of the disc (along the diameter) was removed,
(b) half of the external half of the first Fresnal zone removed (along the diameter)?
View SolutionPlane monochromatic light with intensity I0 falls normally on an opaque disc closing the first Fresnel zone for a point on the screen in front of the wave front. What would be the intensity I at the same point if (a) half of the disc along the diameter were removed, (b) half of the external half is removed along the the diameter ?
View SolutionA plane monochromatic light wave of intensity I0 falls normally on an opaque screen with a long slit having a semicircular cut on one side (Fig.) The edge of the cut coincides with the boundary line of the first Fresnel zone for the observation point P. Thw width of the slit measure 0.90 of the radius of the cut. using Fig. find the intensity of light at the point P.
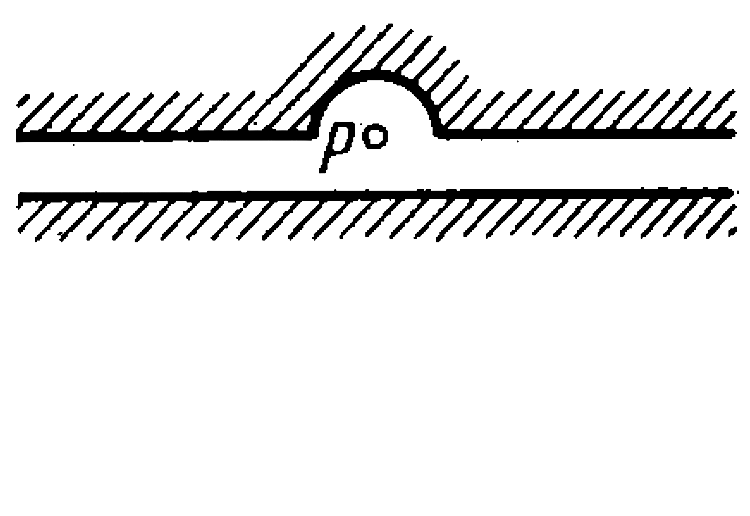

View SolutionA plane monochromatic light wave with intensity I0 falls normally on an opaque screen with a round aperture. What is the intensity of light I behind the screen at the point for which the aperture
(a) is equal to the first Fresnel zone, to the internal half of the first zone,
(b) was made equal to the first Fresnel zone and then half of it was closed (along the diameter) ?
View SolutionA plane light wave with wavelength λ and intensity I0 falls normally on a large glass plate whose opposite side serves as an opaque screen with a round aperture equal to the first Fresnel zone for the observation point P. In the middle of the aperture there is a round recess equal to half the Fresnel zone. What must the depth h of that recess be for the intensity of light at the point P to be the highest? What is this intensity equal to?
View SolutionA plane monochromatic wave of natural light with intensity I0 falls normally on a screen composed of two touching Polaroid half-planes. The principle direction of one Polaroid is parallel,and of the other perpendicular, to the boundary between them. What kind of diffraction pattern is formed behind the screen? What is the intensity of light behind the screen at the points of the plane perpendicualr to the screen and passing through the boundary between the Polaroids?
View SolutionA plane monochromatic light wave falls normally on an opaque screen with a long slit whose shape is shown in Fig. Making use of Fig. find the ratio of intensities of light at points 1,2 and 3 located behind the screen at equal distances from it. For point 3 the rounded-off edge of the slit coincides with the boundary line of the first Fresnel zone.

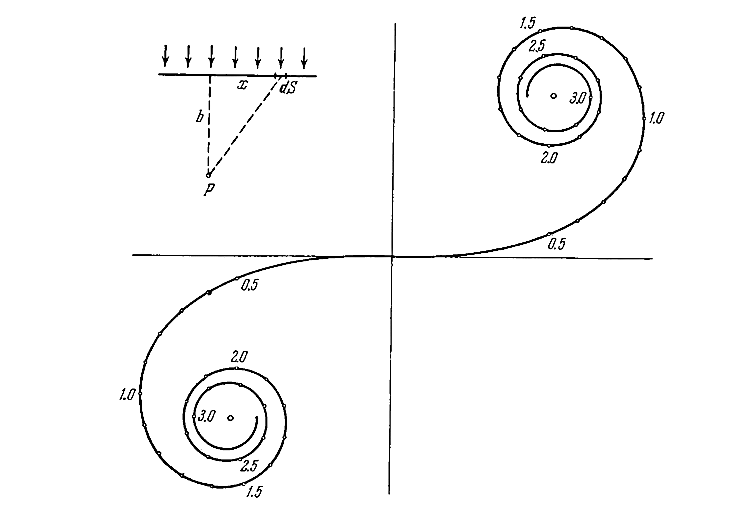
View SolutionA plane monochromatic light wave falls normally on an opaque screen shaped as a long strip with a round hole in the middle. For the observation point P the hole corresponds to half the Fresnel zone, with the hole diameter being η=1.07 times less then the width of the strip. Using Fig. find the intensity of light at the point P provided that the intensity of the incident light is equal to I0.
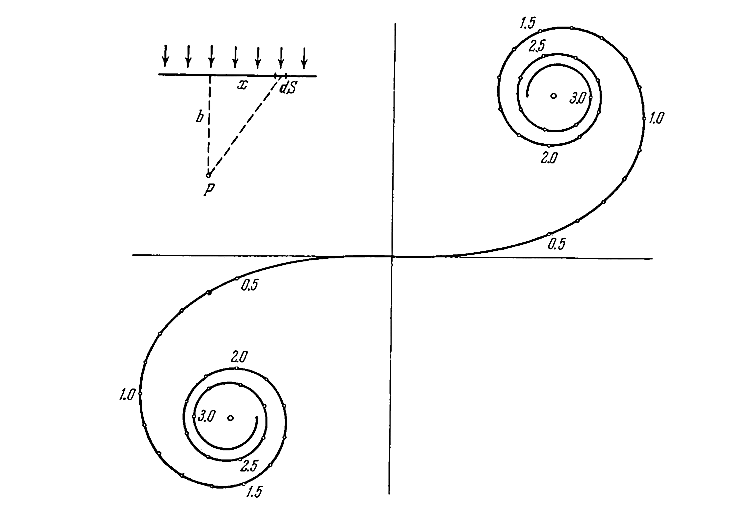
View SolutionA plane monochromatic light wave of intensity I0 falls normally on the surfaces of the opaque screens which are shaped as shown in the figure here. The shaped as shown in the gigure here. The rounded-off edge coinicides with the boundary of the first Fresnel zone. Find the intensity of the screens at a point located behind the point P.
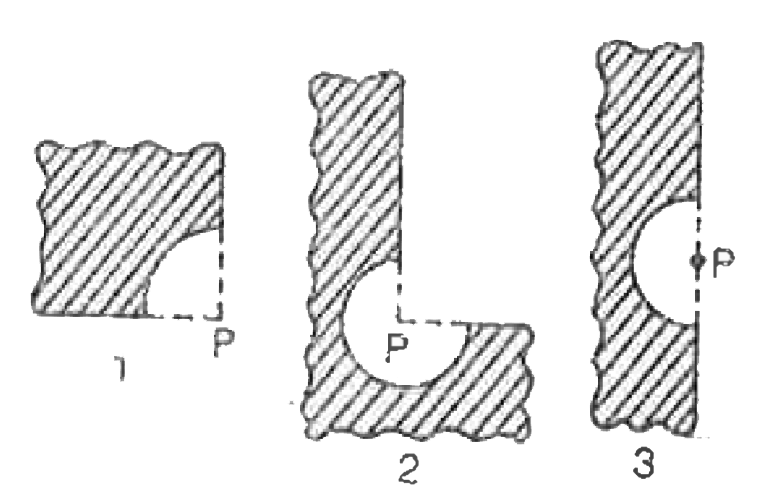
View SolutionA plane monochromatic light wave with intensity I0 falls normally on the surfaces of the opaque screens shown in Fig. Find the intensity of light I at a point P

(a) located behind the corner ponts of screens 1−3 and behind the edge of half-plane 4,
(b) for which the rounded-off edge of screens 5−8 coincides with the boundary of the first formula describing the result obtained for screens 1−4, the same, for screens 5−8.
View Solution
