Using the tables of the Appendix, calculate the difference of refractive indices of quartz for light wavelength $λ = 589.5 n m$ with right-hand and left-hand circular polarizations.

Video Solution

Text Solution

Verified by Experts

Light polarized along the $x$ -direction (i.e. one whose electric vector has only an $x$ component) and propagting along the $z -$ direction can be decomposed into left and right circualry polarized light in accordance with the formula
$E_{x} = \frac{1}{2} (E_{x} - i E_{y}) + \frac{1}{2} (E_{x} - i E_{y})$
On passing through a distance $l$ of an active medium these acquire the phases $δ_{R} = \frac{2 π}{λ} n_{R} l$ and $δ_{1} = \frac{2 π}{λ} n_{1} l$ so we get for the complex amplitude
$E' = \frac{1}{2} (E_{x} + i E_{y}) e_{R}^{i δ_{R}} + \frac{1}{2} (E_{x} + i E_{y}) e_{L}^{i δ_{L}}$
$= e^{l \frac{δ_{R} + δ_{l}}{2}} [\frac{1}{2} (E_{x} + i E_{y}) e^{i δ / 2} + \frac{1}{2} (E_{x} - i E_{y}) e^{- i δ / 2}]$
$= e^{l \frac{δ_{R} + δ_{l}}{2}} [E_{x} cos (\frac{δ}{2}) - E_{y} sin (\frac{δ}{2})], δ = δ_{R} - δ_{L}$ .
Apart from an over all phase $(δ_{R} + δ_{1}) / 2)$ (which is irrelevent) this represents a wave whose plane of polarization has rotated by
$\frac{δ}{2} = \frac{π}{λ} (Δ n) l, Δ n = | n_{R} - n_{1} |$
By definition this equals $α l$ so
$Δ n = \frac{α λ}{π}$
$= \frac{589.5 \times 10^{- 6} m m \times 21.72 d e g / m m}{π} \times \frac{π}{180} (r a d)$
$= \frac{5895 \times 21.72}{180} \times 10^{- 3}$
$= 0.71 \times 10^{- 4}$

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Shown in the figure is a prism of angle $30^{\circ}$ and refractive index $μ_{p} = \sqrt{3}$ . Face AC of the prism is covered with a thin film of refractive index $μ_{f} = 2.2$ A monochromatic light of wavelength $λ$ =550 nm fall on the face AB at an angle of incidence of $60^{\circ}$ Calculate angle of emergence

A $0^{\circ}$
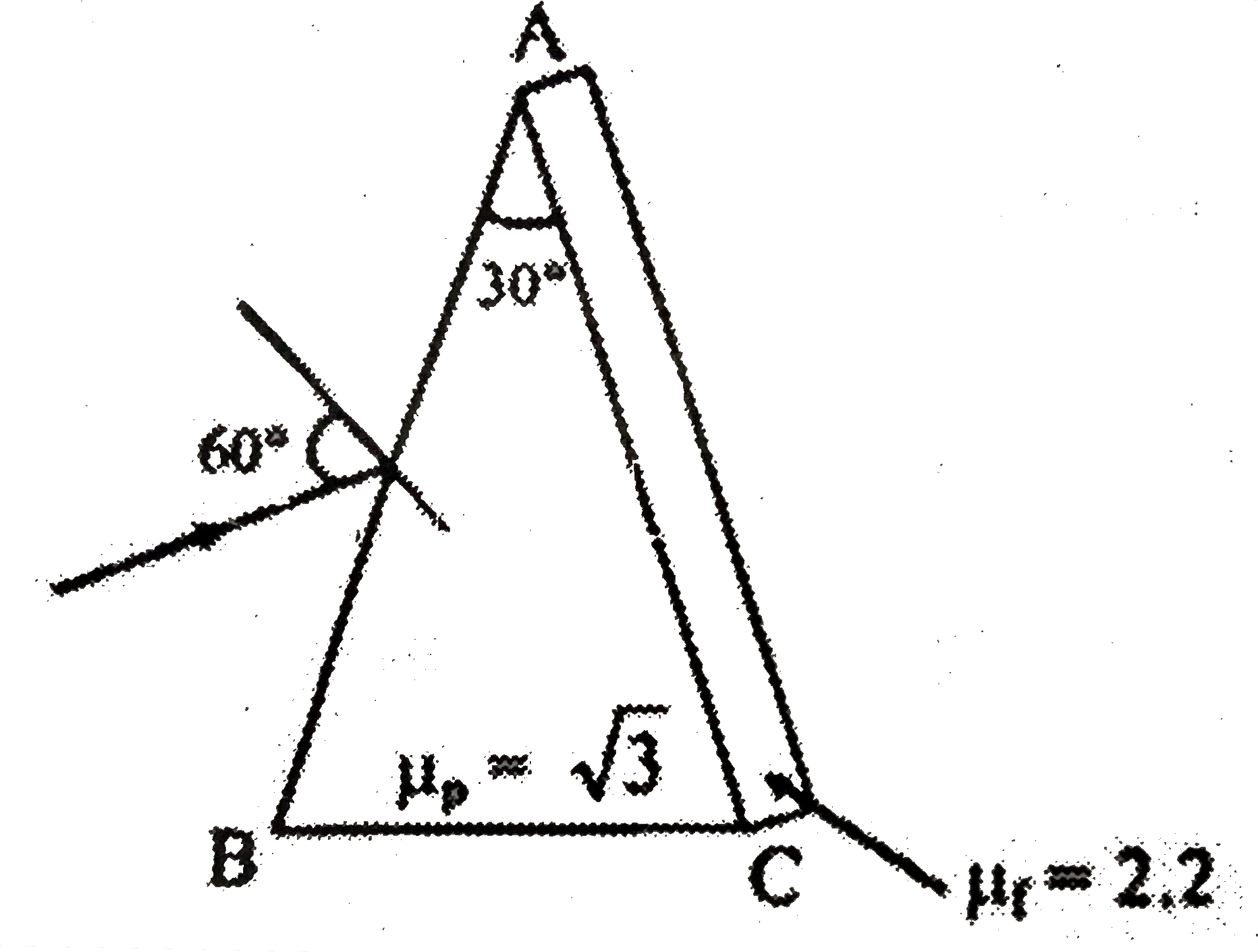B $30^{\circ}$
C $45^{\circ}$
DNot emerge
Question 2 - Select One
Preferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, $θ sin \geq (\frac{1}{μ})$ , get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q An experiment was performed based on the above theory with red, green and blue light. Their refractive indices in the material were 1.39, 1.44 and 1.47, respectively. Which colour would get separated?

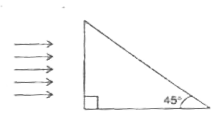Ared
Bgreen
Cblue
Dno colour would be separated.
Question 3 - Select One
Preferential filtering of light consisting of different wavelengths can be done using total internal reflection. The concept of filtering lies in the fact that different wavelengths have different refractive indices in a medium The beam of light with different wavelengths are made incident on an isosceles right angled prism as shown in the figure. The wavelength or wavelengths which satisfy the condition of totai internal reflection, $θ sin \geq (\frac{1}{μ})$ , get reflected
Others get refracted, hence gets separated. G is the angle of incidence and u. is the refractive index .of the particular wavelength in that particular medium. Thus, by changing the medium and by changing the angles of the prism we can satisfy the condition df total internal reflection for a particular wavelength, which gets separated out.
Q If hypothetically the density of the material is increased gradually, then which of the colour gets separated next?

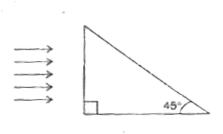Ared
Bgreen
Cblue
Dnone