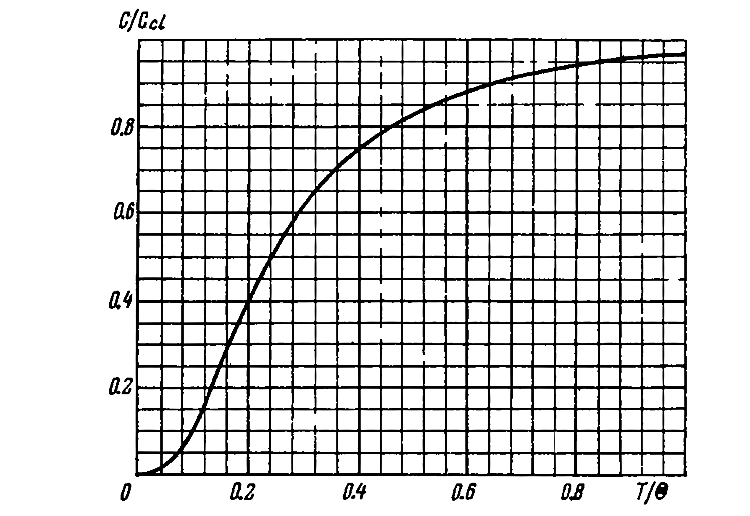
Figure. 6.10 shows heat capacity of a crystal vs temperatue in terms of the Debye theory. Here $C_{c l}$ is classical heat capacity $Θ$ is the Debye temperature. Using this plot, find:
(a0 The Debye temperature for silver if at a temperature $T = 65 K$ its molar heat capacity is equal to $15 J (m o l . K)$ ,
(b) the molar heat capacity of aluminum at $T = 80 K$ if at $T = 250 K$ it is equal to $22.4 J (m o l . K)$
(c )the maximum vibration frequency for copper whose heat capacity at $T = 125 K$ differs form the classical value by $25 %$ .

Text Solution

Verified by Experts

(a) By Dulong and Petit's law, the classical heat capacity is $3 R = 24.94 J / K$ - mol e. Thus
$\frac{C}{C_{c l}} = 0.6014$
From the graph we see that this
value of $\frac{C}{C_{c l}}$ corresponds to $\frac{T}{Θ} = 0.29$
Hence $Θ = \frac{65}{0.29} \approx 224 K$
(b) $22.4 J$ mole - K corresponds to $\frac{22.4}{3 \times 8.314} = 0.898$ . From the graph this corresponds to
$\frac{T}{Θ} \approx 0.65$ . This gives $Θ = \frac{250}{0.65} \approx 385 K$
Then $80 K$ corresponds to $\frac{T}{Θ} = 0.208$
The corresponding value of $\frac{c}{C_{c l}}$ is $0.42$ . Hence $C = 10.5 J / m o l e - K$
(c ) We calculate $Θ$ from the datum that $\frac{C}{C_{c l}} = 0.75 a t T = 125 K$ .
The $x$ -coordinate corresponding to $0.75$ is $0.40$ . Hence
$Θ = \frac{125}{0.4} = 3125 K$
Now $k Θ = ħ ω_{max}$
So $ω_{max} = 4.09 \times 10^{13} r a d / sec$

The molar heat capacity of water is
A $4.184 J K^{- 1}$
B $75.3 J K^{- 1}$
C $85 J K^{- 1}$
D $1 J K^{- 1}$
The molar heat capacity of water is -
A $4.184 J K^{- 1}$
B $75.3 J K^{- 1}$
C $185 J K^{- 1}$
D $1 J K^{- 1}$
Molar heat capacity is
Aextensive property
Bintensive property
Cpath function
Dindependent of temperature