Figure. Illustrates logarithmic electric conductance as a function on reciprocal temperature ( $T$ in $K K$ units) for some

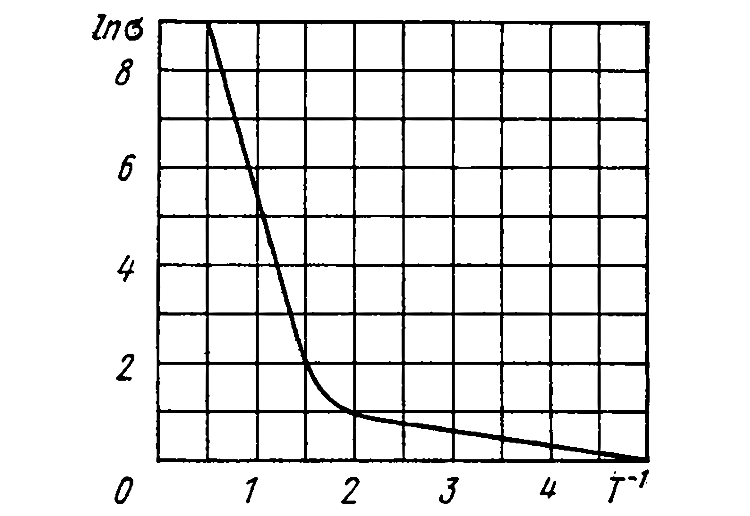
$n$ type semiconductor. Using this plot, find the width of the forbiden band of the semiconductor and the activation energy of donor levels.

Text Solution

Verified by Experts

At high temperatures (small values of $T^{- 1})$ most of the conductivity is infrinsic i.e, it is due to the transition of electrons from the upper levels of the valance band into the lower levels of conduction vands.
For this we can apply approximately the formula
$σ = σ_{0} exp (- \frac{E_{g}}{2 k T})$
or In $σ = I n σ_{0} - \frac{E_{g}}{2 k t}$
From this we get the band gap
$E_{g} = - 2 k \frac{Δ I n σ}{Δ (1 / T)}$
The slope must be calculated at small $\frac{1}{T}$ . Evaluation gives $- \frac{Δ I n σ}{Δ (\frac{1}{T})} = 7000 K$
Hence $E_{g} = 1.21 e V$
At low temperature (high values of $\frac{1}{T})$ the conductance is mostly due to impurities. If $E_{0}$ is the ionization energy of donor levels then we can write the approximate formula (valid at low temperature)
$σ' = σ'_{0} exp (- \frac{E_{0}}{2 k T})$
So $E_{0} = 02 k T \frac{Δ I n σ'}{Δ (\frac{1}{T})}$
The slope must be calculated at low temperatures. Evaluation gives the slope
$- \frac{Δ I n σ'}{Δ (\frac{1}{T})} = \frac{1}{3} \times 1000 K$
Then $E_{0} ~ 0.057 e V$

Updated on:21/07/2023