Find the gratest possible angle through which a deutron is scattered as a result of elastic collision with an initially stationary proton.
From conservation of momentum
√2MTˆi=→pd+→Pp
or P2p=2MT+p2d−2√2MTpdcosθ
From energy conservation
T=p2d2M+p2p2m

(M= mass of denteron, m= mass of proton)
So P2p=2mT−mMp2d
Hence p2d(1+mM)−2√2MTpdcosθ+2(M−m)T=0
For real roots 4(2MT)cos2θ−4×2(M−m)T(1+mM)≥0
cos2θ≥(1−m2M2)
Hence sin2θ≤m2M2
i.e., θ≤sin−1mM
For deuteron-proton scalterting θmax=30∘.
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Elementary Particles
20 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Radioactivity
35 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Find the greatest possible angle through which a deuteron is scattered as result of elastic collision with an initially stationary proton ? Take m1 & m2 as masses of a proton & a deuterium.
View SolutionFind the kinetic energy that must be imparted to a positron for a proton-antiproton pair to be obtained as a result of its collision with a stationary electron.
View Solution
Knowledge Check
A disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
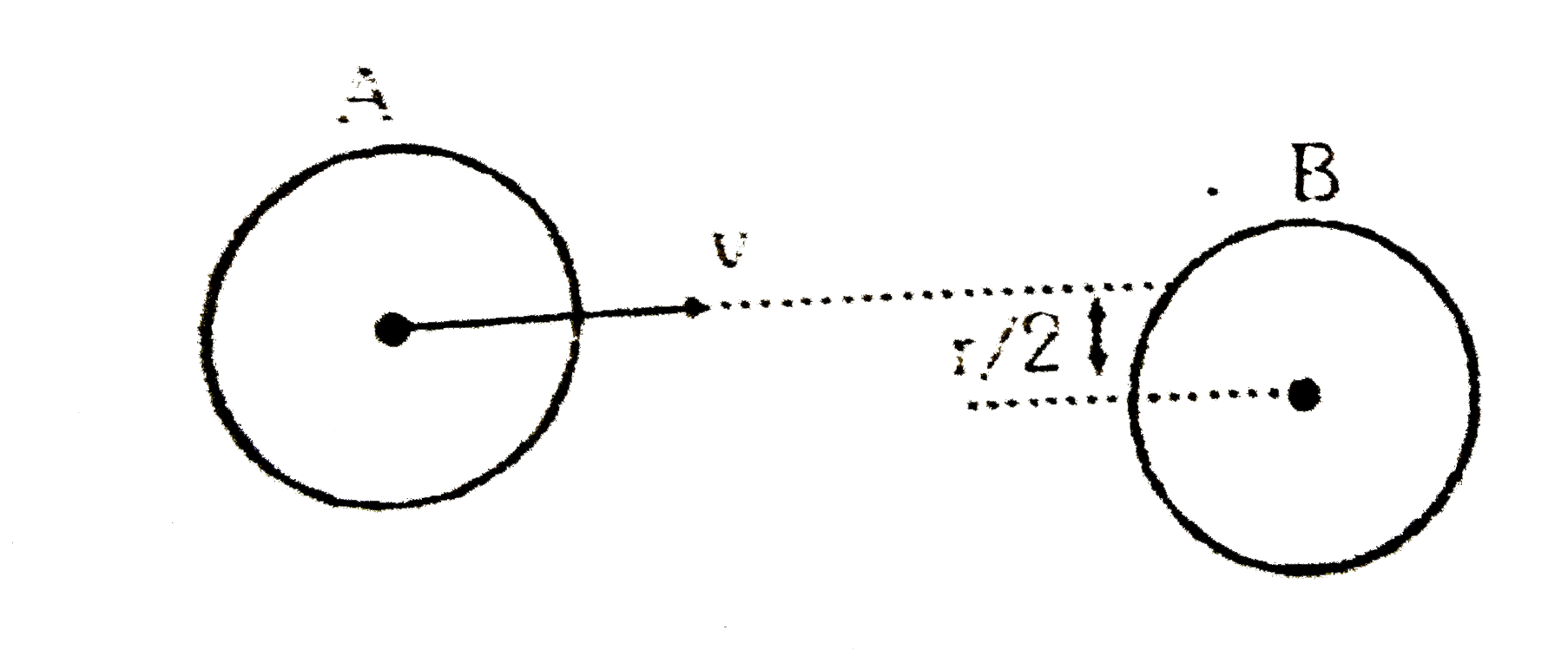 A√154vBv4Cv2D√3v2
A√154vBv4Cv2D√3v2A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘
A disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
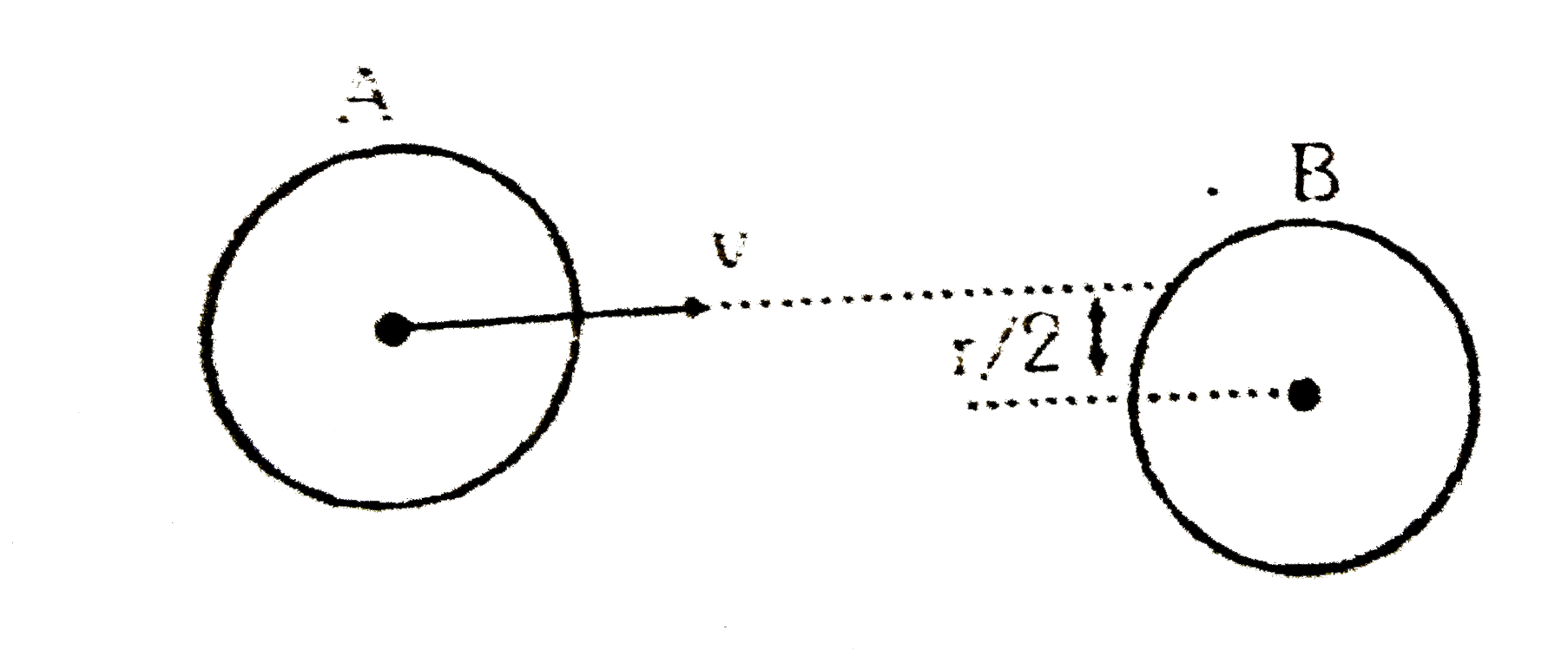
View SolutionA particle of mass m1 collides elastically with a stationary particle of mass m2(m1>m2). Find the maximum angle through which the striking particle may deviate as a result of the collision.
View SolutionAnd α-particle with kinetic enregy Tα=7.0MEV is scattered elastically by an initially stationary .6Li nucleus. Find the kinetic energy of the recoil nucleus if the angle of divergence of the two particles is θ=60∘. Take masses of α partice and lithium as m and M respectively.
View SolutionAn alpha-particle with kinetic energy Tα=7.0MeV is scattered elastically by an initially stationary Li6 nucleus. Find the kinetic energy of the recoil nucleus if the angle of divergence of the two particle is Θ=60∘.
View SolutionA photon of energy hv and momentum hv/c collides with an electron at rest. After the collision, the scattered electron and the scattered photon each make an angle of 45∘ with the initial direction of motion. The ratio of frequency of scattered and incident photon is
View Solution
