A narrow beam of thermal neutrons passes through a plate of iron whose absorption and scattering effective cross-sections are equal to σa=2.5b and σs=11b respectively. Find the fraction of neutrons quitting the beam due to scattering if the thickness of the plate is d=0.50cm.
In traversing a distance d the fraction which is either scattered or absorbed is clearly
1−e−n(σs+σa)d
by the usual definition of the attenuation factor. Of this, the fraction scattered is (by defination of scattering and absorption cross section)
w={1−e−n(σs+σa)d}σsσs+σa
In iron n=ρ×NAM=8.3×1022percc
Substitution gives w=0.352
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ATOMIC AND NUCLEAR PHYSICSExercise:Elementary Particles
Explore 20 Videos
- ATOMIC AND NUCLEAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ATOMIC AND NUCLEAR PHYSICSExercise:Radioactivity
Explore 35 Videos
- DIRECT CURRENTBook:IE IRODOV, LA SENA & SS KROTOVChapter:DIRECT CURRENTExercise:All Questions
Explore 15 Videos
Similar Questions
Detemine how many times the intensity of a narrow beam of thermal neutrons will decrease after passing through the heavy water layer of thickness d=5.0cm. The effective cross-section are of neutrons quitting the beam due to scattering if the thickness of the plate is d=0.50cm. The effective cross-section of interaction of deuterium and oxygen nuclei with thermal neutrons are equal to σ1=7.0b and σs=11b respectivley.
View SolutionA narrow beam of thermal neutrons is attenuated η=360times after passing through a cadmium plate of thickness d=0.50mm. Determine the effective corss-section of interaction of these neutrons with cadmium nuclei.
View Solution
Knowledge Check
The heat is flowing through a rod of length 50 cm and area of cross-section 5cm2 . Its ends are respectively at 25∘C and 125∘C . The coefficient of thermal conductivity of the material of the rod is 0.092kcal/m×s×.∘C . The temperature gradient in the rod is
A2∘C/cmB2∘C/mC20∘C/mD20∘C/cm
A narrow beam of protons with kinetic energy T=1.4meV falls normally on a brass foil whose mass thickness ρd=1.5mg/cm2. The wavelength ratio of copper and zinc in the foil is equal to 7:3 respectively. Find the fraction of the protons scattered through the angles exceeding θ0=30∘.
View SolutionA beam of monochromatic light passes through a pile of N=5 identical plane-parallel glass plates each of thickness l=0.50cm. The coefficient of reflection at each surface of the plates is ρ=0.050. The ratio of the intensity of light transmitted through the pile of plates to the intensity of incident light is τ=0.55 Neglecting the secondary reflections of light, find the absorption coefficient of the given glass.
View SolutionA gold foil of mass m=0.20g was irradiated during t=6.0 hours by a thermal neutron flux falling normally on its suface. Following τ=12hours after the completion of irradiation the activity of the foil became equal to A=1.9.107dis/s. Find the neutron flux density if the effective cross-section of formation of a radioactive nucleus is σ=96b, and the half-life is equal to T=2.7days
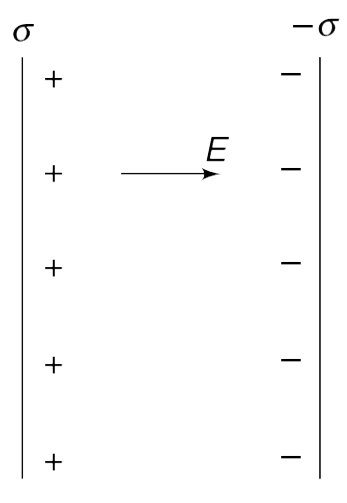
View SolutionTwo students A and B were taught that electric field near a uniformly charged large surface is normal to the surface and is equal to σ2∈0. They were also told that field near the surface of a conductor is σ∈0 normal to the conductor where s is charge density on the conductor surface. Now both of them were asked to write field between the plates of an ideal parallel plate capacitor having charge density σ and −σ on its plates. Student A said that field can be seen as superposition of field due to two large charged surfaces. He wrote the answer as
E=σ2∈0+σ2∈0=σ∈0
Student B thought that a capacitor has conducting plates and therefore field due to each plate
Must be σ∈0 . He wrote his answer as E=σ∈0+σ∈0=2σ∈0
Who is wrong and where is the flaw in thinking ?
View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5cm. If the speed of water at A is 10 cms−1. Find a. the speed at B and b. the difference in pressures at A and B.

View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find a the speed at B and b the difference in pressures at A and B.

View SolutionWater flows through a tube shown in figure. The areas of cross section at A and B are 1cm2and0.5cm2 respectively. The height difference between A and B is 5m. If the speed of water at A is 10 cms−1 find
a) the speed at B.
b) the difference in pressures at A and B.

View Solution
