हल कीजिये:
a) 4(m+3)=18, b) −2(x+3)=8
Step by step video & image solution for हल कीजिये: a) 4(m+3)=18, b) -2(x+3)=8 by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
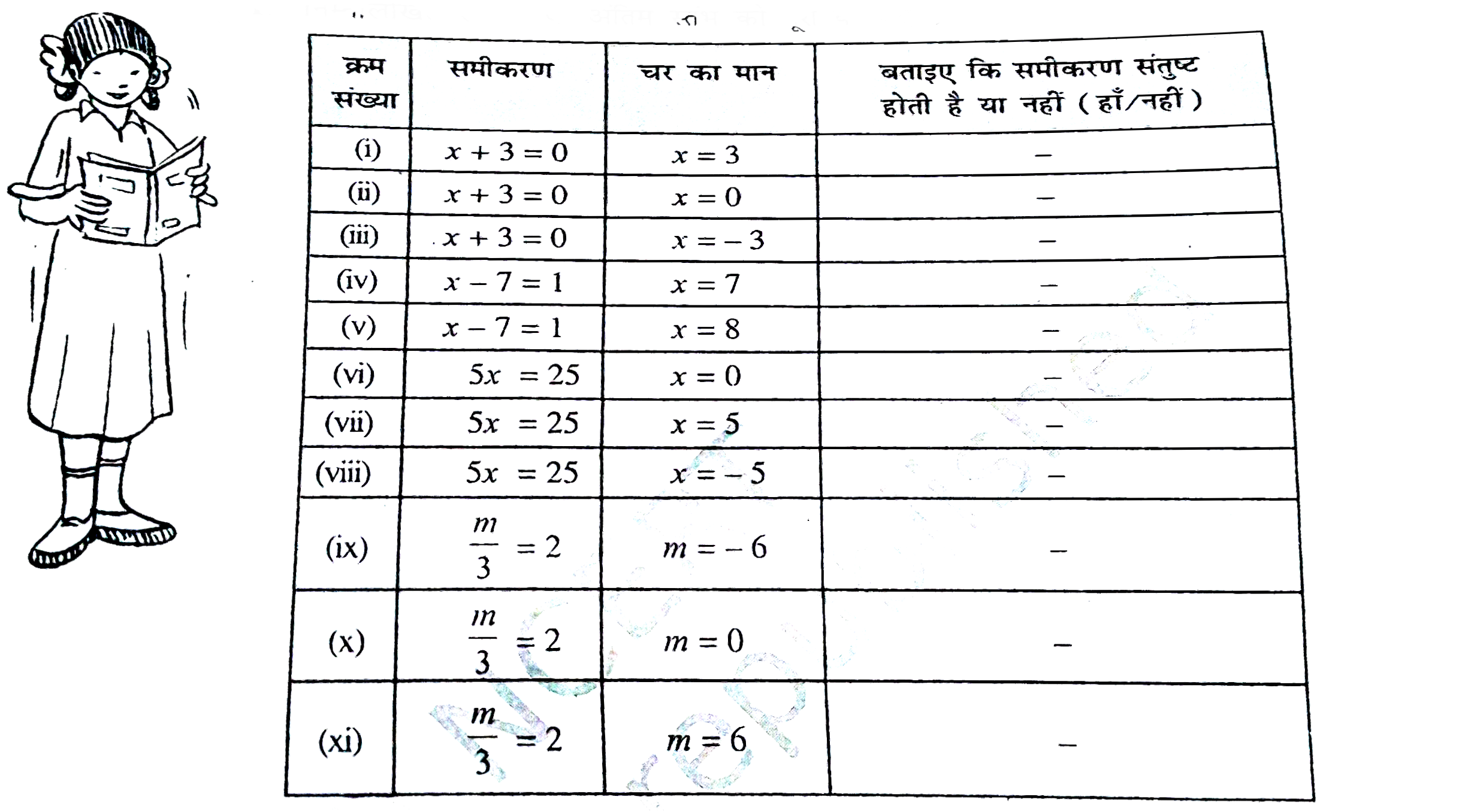
व्यंजक (10y-20) का मान y के मान पर निर्भर करता है। y को पांच भिन्न-भिन्न मान देकर तथा y के प्रत्येक मान के लिए (10y-20) का मान ज्ञात इसकी पृष्टि कीजिये। (10y-20) के प्राप्त किये गए विभिंन मनो से, क्या आप (10y−20)=50 का कोई हल देख रहे है? यदि कोई गाल प्राप्त नहीं हुआ है, तो y को कुछ अन्य मान देकर, ज्ञात कीजिये की प्रतिबन्ध 10y−20=50 संतुष्ट होता है या नहीं।
View Solutionनिम्नलिखित सारणी के अंतिम स्तम्भ को पूरा कीजिये:
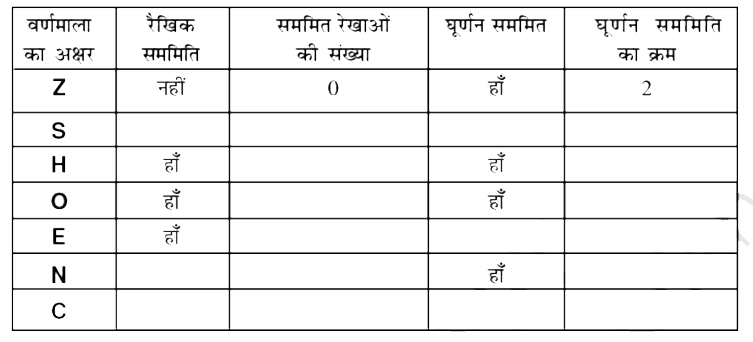
View Solutionअंग्रेजी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएं है। किन बड़े अक्षरों में केवल एक ही सममित रेखा है किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति हैं
उपरोक्त प्रकार से सोचते हुए आप निम्नलिखित सारणी की भरने में समर्थ हो पाएंगें:
View SolutionSolve (a) 4(m+3)=18
(b) −2(x+3)=5
View SolutionLet f(x)=⎧⎨⎩x3+2x2−x−2x3−2x2−x+2for|x|<1x2+ax+bfor|x|≥1 be continuous for all x. Now answer the question:The values of a and b are given by
(A) a=−83,b=−43
(B) a=43,b=−83
(C) a=−43,b=−83
(D) a=−43,b=83
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View Solutionहल कीजिये −8≤5x−3<7.
View Solutionनिम्नलिखित प्रश्न 5 से 16 तक वास्तविक संख्या x के लिए हल कीजिये :
x4<(5x−2)3−(7x−3)5
View Solutionप्रशन 17 से 20 तक की असमिकाओ का हल ज्ञान कीजिये तथा उन्हें रेखा पर आलेखित कीजिये |
3(1−x)<2(x+4)
View Solutionप्रशन 17 से 20 तक की असमिकाओ का हल ज्ञान कीजिये तथा उन्हें रेखा पर आलेखित कीजिये |
x2≥(5x−2)3−(7x−3)5
View Solutionप्रश्न 7 से 10 तक की असमिकाओ को हल कीजिये और उनके हल को संख्या रेखा पर निरूपित कीजिये |
2(x−1)<x+5,3(x+2)>2−x
View Solutionयदि 6 A 11 B 33=18 तथा 4 B 18 A 9=8 हो , तो 3 A 5 B 35=?
View Solutionसमीकरण 5x + 3y = 4 का आलेख खींचिए और जाँच कीजिये कि क्या (a) x = 2, y = 5 और (b) x = -1 और y = 3 समीकरण के हल है ?
View SolutionSolve (a) 4(m+3)=18 (b) −2(x+3)=5
View SolutionThe equation x3=34x=−√38 is satisfied by x=cos(5π18) (b) x=cos(7π18) x=cos(23π18) (d) x=cos(17π18)
View Solution
