एक अध्यापिका दो सेक्शनों के विद्यार्थियों के प्रदर्शनों का विश्लेषण 100 अंक की गणित की परीक्षा लेकर करना चाहती है । उनके प्रदर्शनों को देखने पर वह यह पति है की केवल कुछ ही विद्यार्थियों के प्राप्तांक 20 से कम है और कुछ विद्यार्थियों के प्राप्तांक 70 या उससे अधिक हैं । अतः, उसने विद्यार्थियों को 0-20, 20-30,..., 60-70, 70-100 जैसे विभिन्न माप वाले अंतरालों में वर्गीकृत करने का निर्णय लिया । तब उसने निम्नलिखित सारणी बनाई ।
किसी विद्यार्थी ने इस सारणी का एक आयतचित्र बनाया, जिसे आकृति 14.4 में दिखाया गया है ।

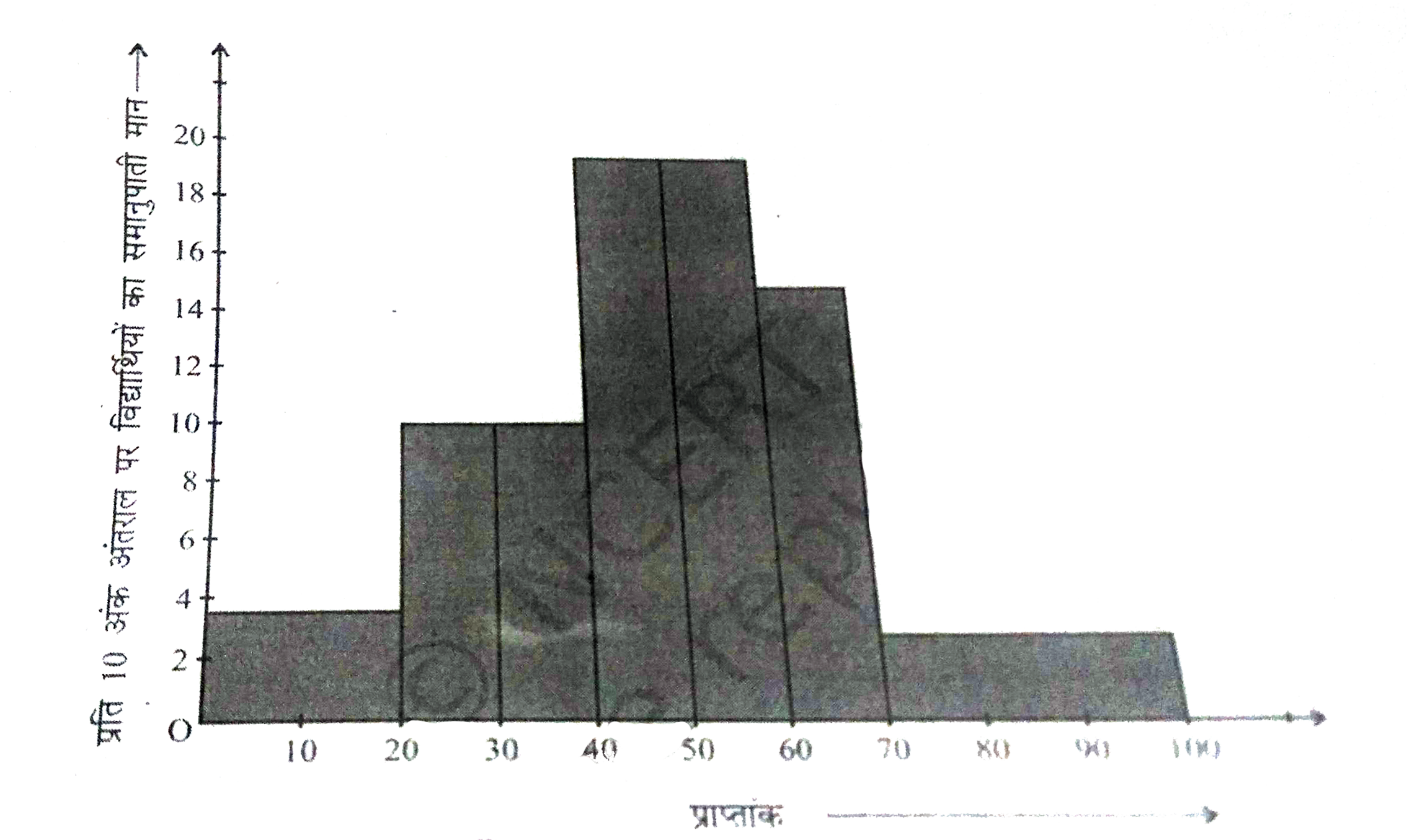
इस आलेखीय निरूपणकी जाँच सावधानी से कीजिए । क्या आप समझते हैं की यह आलेख आकंड़ों का सही-सही निरूपण करता है? इसका उत्तर हैः नहीं । यह आलेख आंकड़ों का एक गलत चित्र प्रस्तुत है । जैसा की हम पहले बता चुके हैं आयतों के क्षेत्रफल आयतचित्र की बारम्बारताओं के समानुपाती होते हैं । पहले इस प्रकार के प्रश्न हमारे सामने नहीं उठे थे, क्योंकि सम्भि आयतों की चौडाईयाँ सामान थी । परन्तु, क्योंकि यहाँ आयतों की चौडाईयाँ बदल रही हैं, इसलिए ऊपर दिया गया आयतचित्र आकंड़ों का एक सही-सही चित्र प्रस्तुत नहीं करता । उदहारण के लिए, यहाँ अंतराल 60 -70 की तुलना में अंतराल 70-100 की बारंबारता अधिक है ।
अतः आयतों की लम्बाइयों में कुछ परिवर्तन (modifications) करने की आवश्यकता होती है, जिससे की क्षेत्रफल पुनः बारम्बारताओं की समानुपाती हो जाये ।
इसके लिए निम्नलिखित चरण लागु करने होते हैः
1. न्यूनतम वर्ग चौड़ाई वाला एक वर्ग अंतराल लीजिए । ऊपर के उदाहरण में, न्यूनतम वर्ग चौड़ाई 10 है ।
2. तब आयतों की लम्बाइयों में इस प्रकार परिवर्तन कीजिए जिससे की वह वर्ग चौड़ाई 10 के समानुपाती हो जाये ।
उदाहरण की लिए, जब वर्ग चौड़ाई 20 होती है, तब आयत की लम्बाई 7 होती है । अतः जब वर्ग चौड़ाई 10 हो, तो आयत की लम्बाई 720×10=3.5 होगी ।
एक प्रक्रिया को लागू करते रहने पर, हमें निम्नलिखित सारणी प्राप्त होती हैः
क्योंकि हमने प्रत्येक स्थिति में 10 अंकों के अंतराल पर ये लम्बाईयाँ परिकलित की हैं, इसलिए आप यह देख सकते हैं की हम इन लम्बाइयों को 'प्रति 10 अंक अंतराल पर विद्यार्थियों के समानुपाती मान' सकते है ।
परिवर्ती चौड़ाई वाला सही आयतचित्र आकृति 14.5 में दिखाया गया है ।
Step by step video & image solution for एक अध्यापिका दो सेक्शनों के विद्यार्थियों के प्रदर्शनों का विश्लेषण 100 अंक की गणित की परीक्षा लेकर करना चाहती है । उनके प्रदर्शनों को देखने पर वह यह पति है की केवल कुछ ही विद्यार्थियों के प्राप्तांक 20 से कम है और कुछ विद्यार्थियों के प्राप्तांक 70 या उससे अधिक हैं । अतः, उसने विद्यार्थियों को 0-20, 20-30,..., 60-70, 70-100 जैसे विभिन्न माप वाले अंतरालों में वर्गीकृत करने का निर्णय लिया । तब उसने निम्नलिखित सारणी बनाई । किसी विद्यार्थी ने इस सारणी का एक आयतचित्र बनाया, जिसे आकृति 14.4 में दिखाया गया है । इस आलेखीय निरूपणकी जाँच सावधानी से कीजिए । क्या आप समझते हैं की यह आलेख आकंड़ों का सही-सही निरूपण करता है? इसका उत्तर हैः नहीं । यह आलेख आंकड़ों का एक गलत चित्र प्रस्तुत है । जैसा की हम पहले बता चुके हैं आयतों के क्षेत्रफल आयतचित्र की बारम्बारताओं के समानुपाती होते हैं । पहले इस प्रकार के प्रश्न हमारे सामने नहीं उठे थे, क्योंकि सम्भि आयतों की चौडाईयाँ सामान थी । परन्तु, क्योंकि यहाँ आयतों की चौडाईयाँ बदल रही हैं, इसलिए ऊपर दिया गया आयतचित्र आकंड़ों का एक सही-सही चित्र प्रस्तुत नहीं करता । उदहारण के लिए, यहाँ अंतराल 60 -70 की तुलना में अंतराल 70-100 की बारंबारता अधिक है । अतः आयतों की लम्बाइयों में कुछ परिवर्तन (modifications) करने की आवश्यकता होती है, जिससे की क्षेत्रफल पुनः बारम्बारताओं की समानुपाती हो जाये । इसके लिए निम्नलिखित चरण लागु करने होते हैः 1. न्यूनतम वर्ग चौड़ाई वाला एक वर्ग अंतराल लीजिए । ऊपर के उदाहरण में, न्यूनतम वर्ग चौड़ाई 10 है । 2. तब आयतों की लम्बाइयों में इस प्रकार परिवर्तन कीजिए जिससे की वह वर्ग चौड़ाई 10 के समानुपाती हो जाये । उदाहरण की लिए, जब वर्ग चौड़ाई 20 होती है, तब आयत की लम्बाई 7 होती है । अतः जब वर्ग चौड़ाई 10 हो, तो आयत की लम्बाई (7)/(20) xx 10 = 3.5 होगी । एक प्रक्रिया को लागू करते रहने पर, हमें निम्नलिखित सारणी प्राप्त होती हैः क्योंकि हमने प्रत्येक स्थिति में 10 अंकों के अंतराल पर ये लम्बाईयाँ परिकलित की हैं, इसलिए आप यह देख सकते हैं की हम इन लम्बाइयों को 'प्रति 10 अंक अंतराल पर विद्यार्थियों के समानुपाती मान' सकते है । परिवर्ती चौड़ाई वाला सही आयतचित्र आकृति 14.5 में दिखाया गया है । by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सांख्यिकीBOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.1
2 Videos
- सांख्यिकीBOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.2
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.4
8 Videos
- हीरोन का सूत्र BOOK - NCERT HINDICHAPTER - हीरोन का सूत्र EXERCISE - प्रश्नावली 12.2
9 Videos
Similar Questions
उन आंकड़ों के पाँच उदाहरण दीजिए जिन्हे आप अपने दैनिक जीवन से एकत्रित कर सकते हैं।
View Solutionआठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैः
A,B,O,O,AB,O,A,O,B,A,O,B,A,O,OA,AB,O,A,A,O,O,AB,B,A,O,B,A,B,O
इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए की इन विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।
View Solutionसमांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है । दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है ।
View Solutionएक पार्क चतुर्भुज ABCD के आकार का है, जिसमे ∠C=90∘,AB=9 मी, BC=12 मी, CD=5 मी और AD=8 मी है। इस पार्क का कितना क्षेत्रफल है?
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionविद्यालय के वार्षिकोत्सव के अवसर पर विद्यार्थियों द्वारा निर्मित हस्तकला की वस्तुओं की प्रदर्शनी के प्रचार हेतु लगभग 50 शब्दों में एक विज्ञापन लिखिए।
View Solutionविद्यालय में वार्षिकोत्सव के अवसर पर विद्यार्थियों द्वारा निर्मित हस्तकला की वस्तुओं की प्रदर्शनी के लिए एक विज्ञापन लगभग 25-50 शब्दों में तैयार कीजिए।
View Solutionनिम्नलिखित विषयों में से किसी एक पर संकेत बिन्दुओं के आधार पर लगभग 100 शब्दों में अनुच्छेद लिखिए :
कम्प्यूटर हमारा मित्र
• क्या है
• विद्यार्थियों के लिए उपयोग
• सुझाव
View Solutionवर्गीकृत आंकड़ों की 'से कम प्रकार' और 'से अधिक प्रकर' की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के 'भुज' से प्राप्त होता है आंकड़ों का----
View SolutionThe average of the test scores of a class of 'm' students is 70 and that of ’n' students is 91. When the scores of both the classes are combined, the average is 80. What is n/m? m विद्यार्थियों की कक्षा के प्राप्तांकों का औसत 70 है तथा n विद्यार्थियों का 91 है। जब दोनों कक्षाओं के अंको को जोड़ दिया जाए तो ओसत 80 है। n/m का मान ज्ञात करें?
View Solution'भाषा की नियमबद्ध प्रवृत्ति को पहचानना और उसका विश्लेषण करना' उच्च प्राथमिक स्तर के भाषा -शिक्षण का एक ________ उद्देश्य है।
View Solutionविद्यार्थियों की एक पंक्ति में , सोहन का स्थान दोनों मे से किसी भी किनारे से 9 वाँ है तब विद्यार्थियों की कुल संख्या होगी ?
View Solutionविद्यार्थियों में भाषा की रुचि का विकास करने का उपयुक्त उपाय है
View SolutionThe given Bar Graph presents the number of students of two schools for six years. दिया गया दंड आरेख (बार ग्राफ) छह वर्षो के दौरान दो स्कूलों में विद्यार्थियों की संख्या को दर्शाता है| What is the average number of students from school B during the six year period (correct to two decimal places)? छह वर्षों की अवधि के दौरान स्कूल B के विद्यार्थियों की औसत संख्या कितनी है [दो दशमलव स्थानों तक सही )?
View SolutionThe given Bar Graph presents the number of students of two schools for six years. दिया गया दंड आरेख (बार ग्राफ) छह वर्षो के दौरान दो स्कूलों में विद्यार्थियों की संख्या को दर्शाता है| In which year, the percentage increase in students in school B is the highest in comparison to its previous year? किस वर्ष में, स्कूल B के विद्यार्थियों की संख्या में प्रतिशत वृद्धि इसके पिछले वर्ष की तुलना में सबसे अधिक है?
View Solution