To construct a triangle given its base, a base angle and the difference of the other two sides.
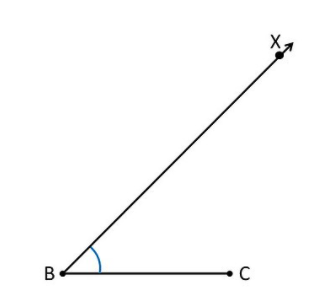
Draw a base BC
Draw ∠B. Let the ray be BX
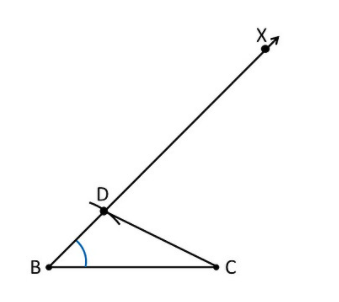
Open the compass to length AB−AC. From point B as center, cut an arc on ray BX. Let the arc intersect BX Let the arc intersect BX at D. Join CD.
We will draw perpendicular bisector intersects BD. Join AC.
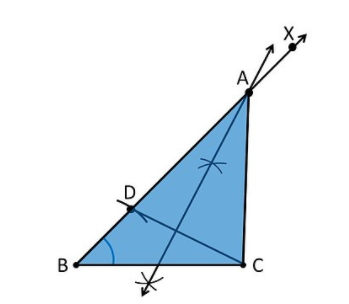
△ABC is the required triangle.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - Example
1 Videos
- CONSTRUCTIONSBOOK - NCERTCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.1
5 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
- COORDINATE GEOMETRYBOOK - NCERTCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2
2 Videos
Similar Questions
Exercise-11.1 Discussion|| Construction OF Triangles|| 1 - To construct a triangle|| Given its base|| A Base angle and Sum OF Other Two sides|| 2 - To construct A Triangle||given its base|| A Base angle and The Difference OF other Two sides ABAC
View SolutionTo construct a triangle, given its base, a base angle and sum of other two sides.
View Solution
Knowledge Check
Two sides of a triangle are 10 cm and 15 cm and the base is 20 cm long . If another triangle similar to the first triangle has the base measuring 32 cm , then other two sides of the triangle are
A16 cm , 24 cmB12 cm , 28 cmC15 cm , 25 cmD18 cm , 22 cm
To construct a triangle, given its perimeter and its two base angles.
View SolutionConstruct a right triangle whose base is 4cm and the sum of its hypotenuse and the other side is 8cm.
View SolutionThe altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
View SolutionConstruct an equilateral triangle, given its side and justify the construction.
View SolutionOne side of a right angled triangle is 20 cm and the difference in lengths of its hypotenuses & other side is 8cm. Find the other side and area of the triangle.
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one half of the vertical angle.
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one-half of the vertical angle.
View Solution
