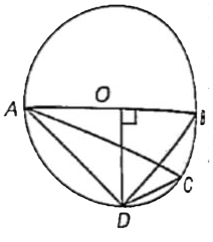
In the given figure, ABC and AED are straight lines. AB is the diameter of the smaller circle ABE. Find the measure of ∠ACD.
Video Solution
Text Solution
As AB is the diameter of the smaller circle,
∴∠AEB=90∘
As, AED is a straight line,
∴∠AEB+∠DEB=180∘
⇒∠DEB=180∘−90∘=90∘
Now, BEDC is a cyclic quadrilateral.
∴∠DEB+∠BCD=180∘
⇒90∘+∠BCD=180∘
⇒∠BCD=90∘
Also, ∠ACD=∠BCD
∴∠ACD=90∘
|
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
 A30∘B60∘C45∘D25∘
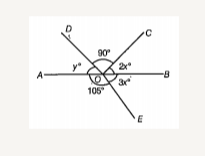
A30∘B60∘C45∘D25∘In the following figure AB is a straight line. Find (x+y):
 A55∘B65∘C75∘D80∘
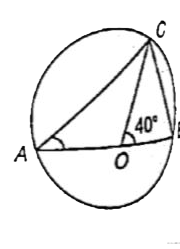
A55∘B65∘C75∘D80∘In the given figure, ∠COB=40∘, AB is the diameter of the circle. Find ∠CAB :
 A40∘B20∘C30∘Dnone of the above
A40∘B20∘C30∘Dnone of the above
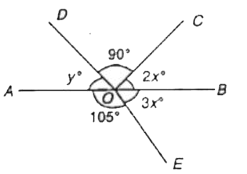
In a figure , AB is a straight line , Find (x+y):
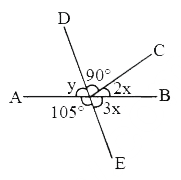
View SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find ∠CAB:

View SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find m∠CAB:

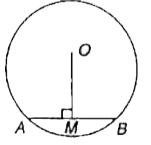
View SolutionIn the given figure OM⊥AB, radius of the circle is 5 cm and length of the chord AB=8cm. Find the measure of OM:
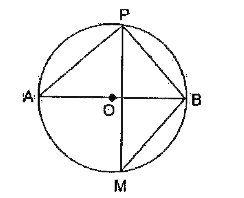
View SolutionIn the given figure, if AB is the diameter of the circle and PM the internal bisector of ∠APB, then the measure of angle ABM is
View Solution