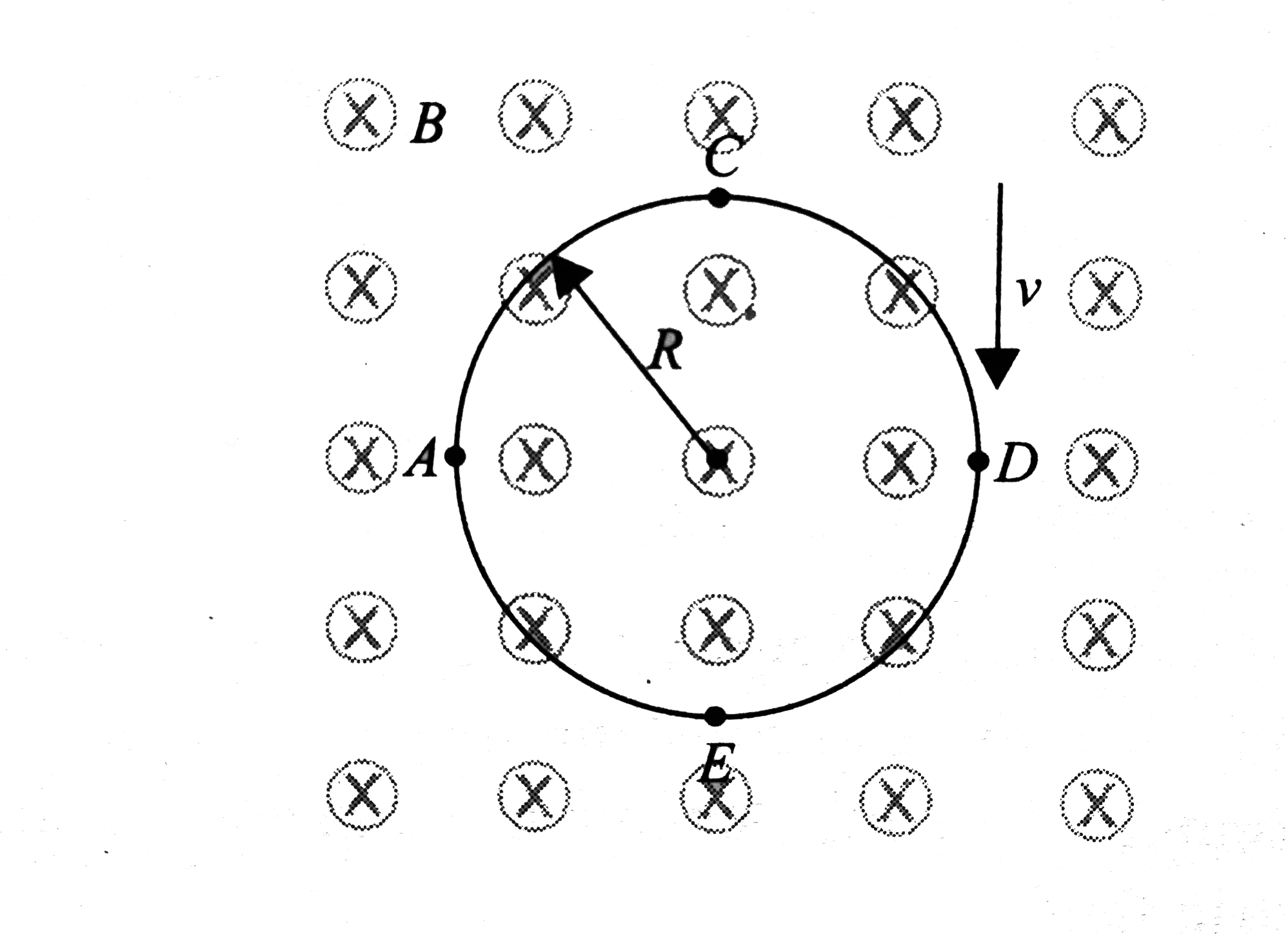
A thin semicircular conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in The potential difference developed across the ring when its speed is v, is
zero
Bvπr22 and P is at higher potential
πrBv and R is at higher potential
2rBv and R is at higher potential
The correct Answer is:D
|e|=dϕdt=ddt(BA)=BdAdt
=B× diameter × velocity =B×2r×v=2rvB
According to Fleming's right hadn rule, if P and R are connected to a closed external circuit, the direction of the induced current is from P to R. In the external circuit, the current is from R to P so the potential of R is greater than that of P.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NEET
4 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - CBSE SCANNER
28 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - JEE Main
1 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
Similar Questions
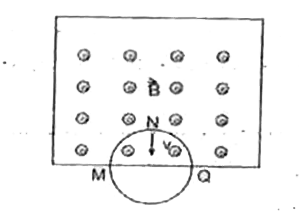
A thin semicircular conducting ring of radius R is falling with its plane verticle in a horizontal magnetic inducting B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is
(1.) zero
(2.)BcπR2/2
(3.) πRBV
(4.) 2RBV
View SolutionA thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ shown in the fig, the speed of the ring is V. The potential difference developed across the semicircular ring is
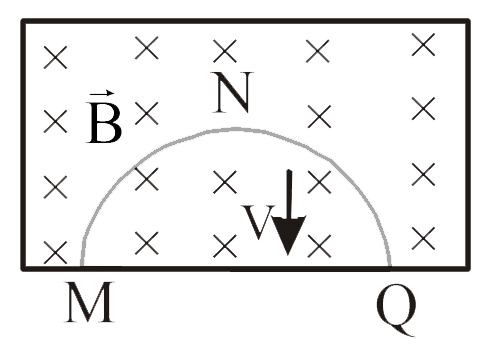
View Solution
Knowledge Check
A thin semicircuilar conducting ring (PQR) of radius r is falling with its plane vertical in a horizontal magnetic field B, as shown in Fig. The potential difference developed across the ring when its speed is υ, is
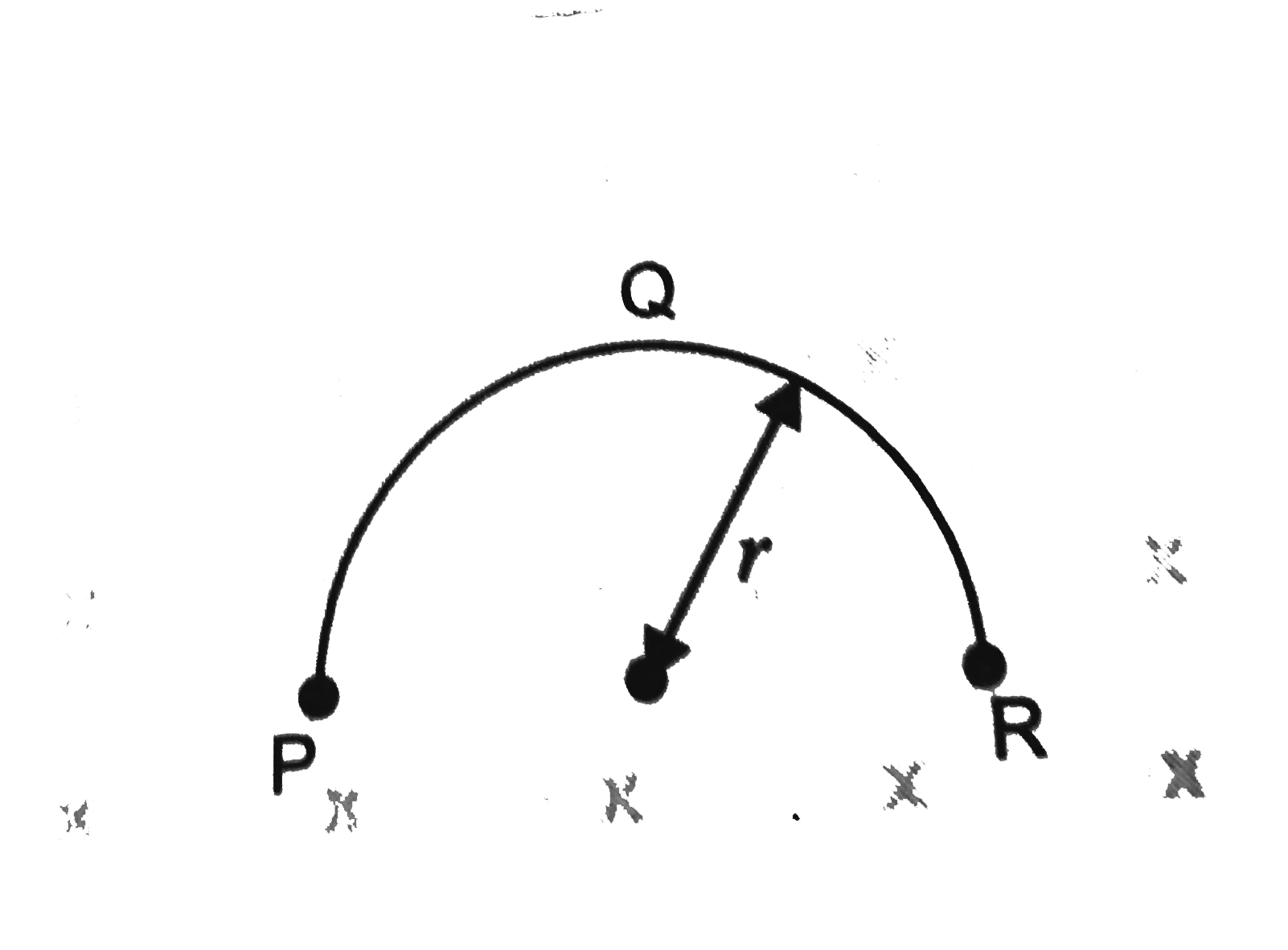AzeroBBυπr2 and P is at higher potentialCπrBυ and R is at higher potentialD2rBυ and R is at higher potentialA thin semicircular conducting ring of radius R is falling with its plane vertical in a horizontal magnetic induction B. At the position MNQ, the speed of the ring is V and the potential difference developed across the ring is
AZeroBBvπR2/2 and M is at higer potentialCπRBV and Q is at higer potentialD2RBV and Q is at higer potentialA thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
AZeroBBvπR2N2 and M is at higher potentialCNπ BRv and Q is at higher potentialD2RBvN and Q is at lower potential
A thin circular -conducting ring having N turns of radius R is falling with its plane vertical in a horizontal magnetic field B . At the position MNQ the speed of ring is v the induced e.m.f developed across the ring is
View SolutionA thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
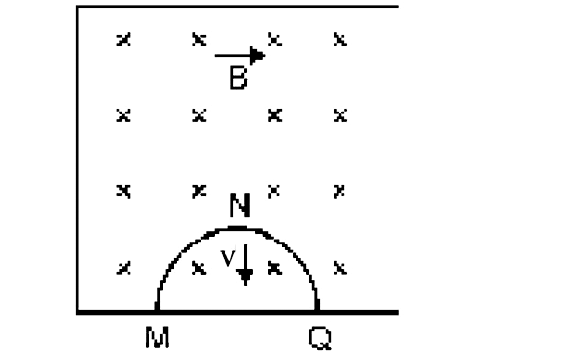
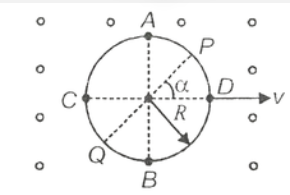
View SolutionA conducting ring of radius R is being moved in a region of uniform magnetic field as shown. Let EAB represent the potential difference between A and B then
View SolutionA thin semi-circular conducting ring of radius R is falling with its plane verticle in horizontal magnetic induction (→B). At the position MNQ the speed of the ring is v, and the potential difference developed across the ring is
View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,
View Solution