Let ABCandPQR be any two triangles in the same plane. Assume that the perpendiculars from the points A,B,C to the sides QR,RP,PQ respectively are concurrent. Using vector methods or otherwise,prove that the perpendiculars from P,Q,R→BC,CA,AB respectively are also concurrent.
Step by step video & image solution for Let ABC and PQR be any two triangles in the same plane. Assume that the perpendiculars from the points A, B, C to the sides QR, RP, PQ respectively are concurrent. Using vector methods or otherwise,prove that the perpendiculars from P, Q, R to BC, CA, AB respectively are also concurrent. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In a ΔABC right angle at C .P is the length of ⊥ from C to AB. If a, b, c, are the length of BC , CA, AB. Which relation is correct .
A1p2=1b2−1a2B1p2=1a2+1b2C1p2+1a2=−1b2D1p2=1a2−1b2Let →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
Aa.b+b.c+c.a=0Ba×b=b×c=c×aCa.b=b.c=c.aDa×b+b×c+c×a=0
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
View SolutionTwo triangles ABC and PQR are such that the perpendiculars from A to QR ,B to RP and C to PQ are concurrent .Show that the perpendicular from P to BC ,Q to CA and R to AB are also concurrent .
View SolutionD,E,F are the foot of the perpendiculars from vertices A,B,C to sides BC,CA,AB respectively, and H is the or the centre of acute angled triangle ABC, where a,b,c are the sides of triangle ABC, then
View SolutionA triangle ABC has ∠B=∠C. Prove that :
(i) the perpendiculars from the mid-point of BC to AB and AC are equal.
(ii) the perpendicular from B and C to the opposite sides are equal.
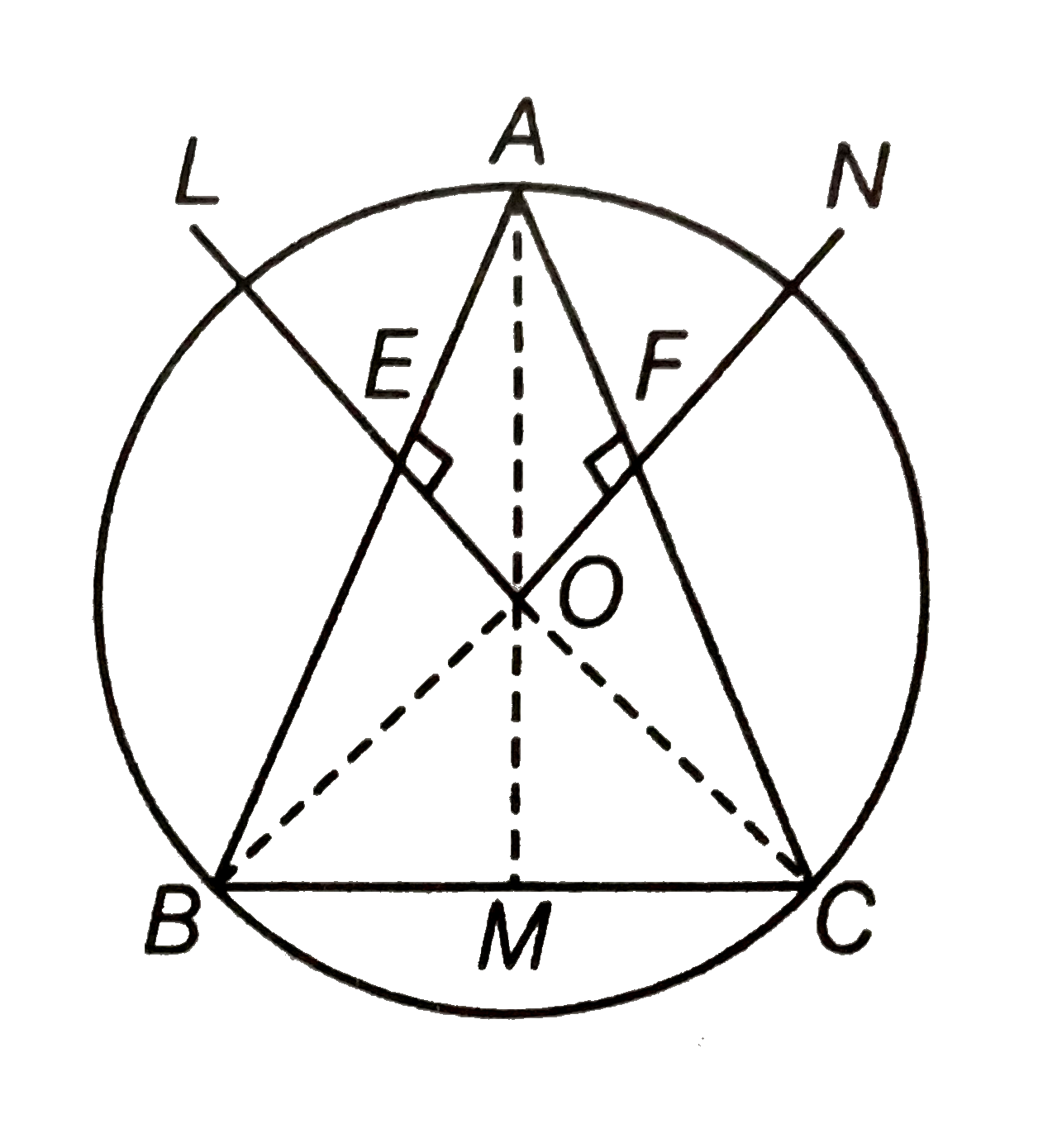
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View Solution
