Point 'O' is the centre of the ellipse with major axis AB & minor axis CD. Point F is one focus of the ellipse. If OF = 6 & the diameter of the inscribed circle of triangle OCF is 2, then find the product (AB).(CD)
Step by step video & image solution for Point 'O' is the centre of the ellipse with major axis AB & minor axis CD. Point F is one focus of the ellipse. If OF = 6 & the diameter of the inscribed circle of triangle OCF is 2, then find the product (AB).(CD) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If the minor axis of an ellipse subtends an equilateral triangle with vertex at one end of major axis, then write the eccentricity of the ellipse.
View Solutionबिन्दु 'O' दीर्घवृत्त का केन्द्र तथा AB तथा CD क्रमशः दीर्घअक्ष तथा लघुअक्ष है। बिन्दु F दीर्घवृत्त की एक नाभि है। यदि OF = 6 तथा त्रिभुज OCF के अन्तःवृत्त का व्यास 2 हो, तो (AB) (CD) का गुणनफल ज्ञात कीजिये।
View SolutionIn an ellipse, if the lines joining focus to the extremities of the minor axis form an equilateral triangle with the minor axis, then the eccentricity of the ellipse is
View Solutionदीर्घवृत्त जिसका दीर्घ अक्ष AB तथा लघु अक्ष CD है, का केन्द्र बिन्दु O है। बिन्दु F दीर्घवृत्त की एक नाभि है। यदि OF = 6 तथा त्रिभुज OCF के अन्तर्गत वृत्त का व्यास 2 है, तो गुणनफल (AB)(CD) है -
View SolutionFind the equations of the ellipse whose end points of major axis are (±3,0) and end points of minor axis are (0,±2)
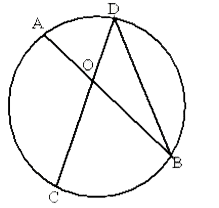
View SolutionAB is a diameter of the circle. Two points C and D are such point that CD = BD. AB and CD intersect at O. If angle ∠AOD=45∘. Find ∠ADC
View SolutionIn an ellipse if the lines joining focus to the extremities of the minor axis from an equilateral triangle with the minor axis then find the eccentricity of the ellipse.
View SolutionConsider an ellipse E:x2a2+y2b2=1, centered at point 'O' and having AB and CD as its major and minor axes respectively if S1be one of the focus of the ellipse, radius of the incircle of ΔOCS1 be 1 unit and OS1=6units. Q. The equation of the director circle of (E) is
View Solution
