lf circular arcs ¯¯¯¯¯¯ACand¯¯¯¯¯¯BC have centres at B(−α,0)andA(α,0) respectively and equation of circle which touches both arcs ¯¯¯¯¯¯ACand¯¯¯¯¯¯BC and line AB is (x−a)2+(y−b)2=r2,r>0, if length of arc BC=8π, the value of |a+b+r−α| equals
Step by step video & image solution for lf circular arcs overline(AC) and overline(BC) have centres at B(-alpha, 0) and A(alpha, 0) respectively and equation of circle which touches both arcs overline(AC) and overline(BC) and line AB is (x-a)^2+ (y-b)^2=r^2,r>0, if length of arc BC=8pi, the value of |a+b+r-alpha| equals by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The endpoints of ¯¯¯¯¯¯AB are A(0, 0) and B(9, -6). What is an equation of the line that contains the reflection of ¯¯¯¯¯¯AB in the y-axis?
Ay=−32xBy=−23xCy=−x+3Dy=23xIf ¯a,¯b,¯c are position vectors of points A, B, C respectively such that 5¯a−3¯b−2¯c=0, then
AC divides BA in internally in the ratio 5:3BC divides BA in externally in the ratio 5:3CC divides AB in internally in the ratio 5:3DC divides AB in internally in the ratio 5:3If ¯a,¯b,¯c are non-coplanar and m, n are real numbers, the [m¯am¯b3¯c]−[m¯b¯cn¯a]−[n¯cn¯a2¯b]=0 is true for
Aexactly one value of m, nBexactly two value of m, nCexactly three values of m, nDall values of m, n
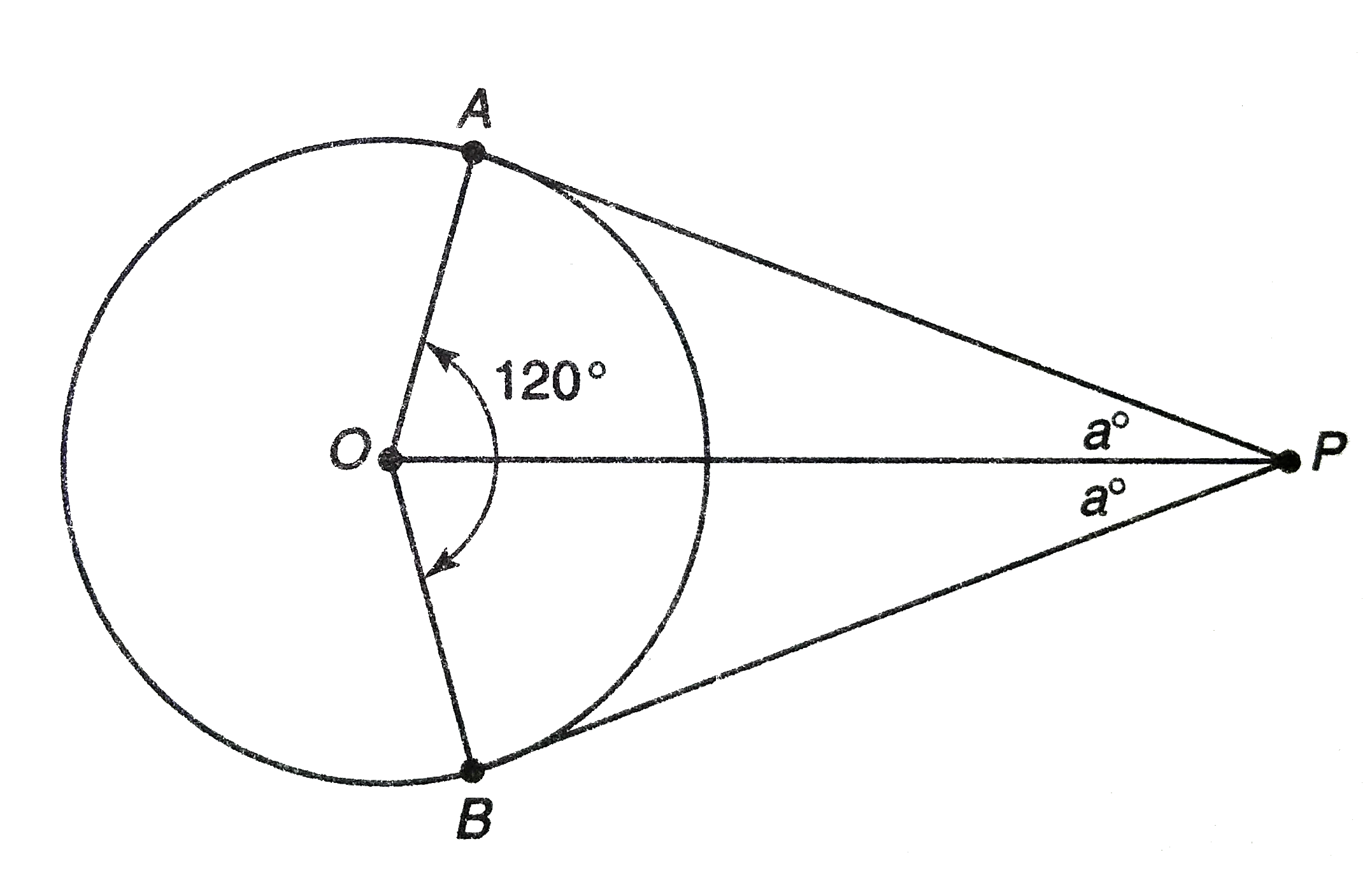
In the figure above, ¯¯¯¯¯¯PA is tangent to circle O at point A, ¯¯¯¯¯¯PB is tangent to circle O at point B. Angle AOB measures 120∘ and OP=4π. What is the length of minor arc AB?
View SolutionIf ¯a,¯b,¯c are non-coplanar vectors, then the vectors given by ¯p=2¯a−2¯c,¯q=3¯a+¯b+5¯cand¯r=2¯a−4¯b+3¯c are
View SolutionIf the points A(¯a),B(¯b),C(¯c) are collinear and 3¯a+2¯b−5¯c=¯0, then
View SolutionP, Q, R are the mid-points of the sides BC, AC, and AB respectively of △ABC. If G1(¯¯¯g1)andG2(¯¯¯g2) are the centroids of the △ABCand△PQR respectively, then
View SolutionIn △ABC, if the points P, Q, R divides the sides BC, CA, AB in the ratio 1:4, 3:2, 3:7 respectively and the point S divides side AB in the ratio 1:3, then (¯¯¯¯¯¯AP+¯¯¯¯¯¯BQ+¯¯¯¯¯¯CR):(¯¯¯¯¯CS)=
View Solution