दो बिन्दु आवेश, प्रत्येक q, क्रमशः (0, a) तथा (0, - a) पर रखे हैं। बिन्दु (a,0) पर परिणामी विद्युत् क्षेत्र की गणना कीजिए।

Video Solution

Text Solution

Verified by Experts

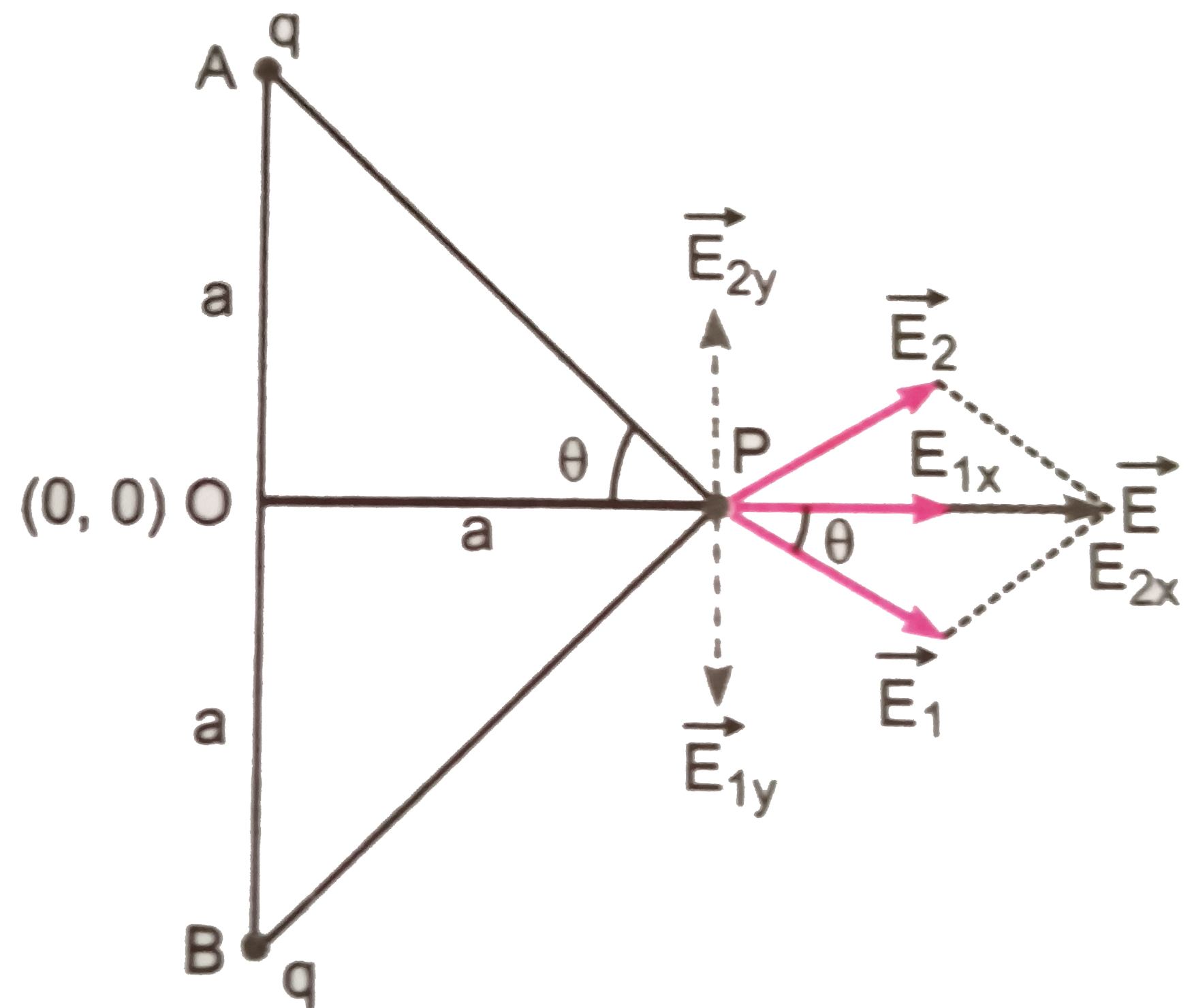
चित्र 1.23 में आवेश q बिन्दु A (0, a) पर तथा आवेश q बिन्दु B (0, - a) पर स्थित है। हमें बिन्दु P (a, 0) पर विद्युत् क्षेत्र की गणना करनी है।
चित्र से स्पष्ट है कि $A P = B P = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$
बिन्दु A पर स्थित आवेश q के कारण बिन्दु P पर विद्युत् क्षेत्र
$- \to E_{1} = \frac{1}{4 π ε_{0}} \frac{q}{{(A P)}^{2}} = \frac{1}{8 π ε_{0}} \frac{q}{a^{2}}$ (दिशा $- - \to A P$ में)
बिन्दु B पर स्थित आवेश q के कारण बिन्दु P पर विद्युत् क्षेत्र
$- \to E_{2} = \frac{1}{4 π ε_{0}} \frac{q}{{(B P)}^{2}} = \frac{1}{8 π ε_{0}} \frac{q}{a^{2}}$ (दिशा $- - \to B P$ में)
स्पष्टतः $- \to E_{1}$ तथा $- \to E_{2}$ परिमाण में समान हैं।
$- \to E_{1}$ व $- \to E_{2}$ को क्षैतिज व ऊर्ध्वाधर घटकों में वियोजित करने पर हम पाते हैं कि इनके ऊर्ध्वाधर घटक परस्पर विपरीत दिशा में होने के कारण निष्फल हो जाते हैं तथा क्षैतिज घटक समान दिशा में होने के कारण परस्पर जुड़ जाते हैं। अत: बिन्दु P पर परिणामी विद्युत् क्षेत्र
$\to E = - - \to E_{1 x} + - - \to E_{2 x} = E_{1} cos θ + E_{2} cos θ,$ जहाँ $cos θ = \frac{O P}{A P} = \frac{a}{a \sqrt{2}} = \frac{1}{\sqrt{2}}$
$= 2 E_{1} cos θ$ (क्योंकि $- \to E_{1} = - \to E_{2}$ परिमाण में)
$= 2 \times \frac{1}{8 π ε_{0}} \frac{q}{a^{2}} \times \frac{1}{\sqrt{2}} = \frac{q}{4 \sqrt{2} π ε_{0} a^{2}}$ (दिशा $- - \to O P$ में)।

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

SHIVLAAL PUBLICATION-विद्युत् आवेश तथा क्षेत्र -वस्तुनिष्ठ प्रश्न

Home
Ask Doubt
Profile