एकसमान आवेशित छड़ जिसकी लम्बाई 2l तथा कुल आवेश q है, के कारण उसके लम्ब समद्विभाजक पर दूरी r पर स्थित किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता ज्ञात कीजिए।
चित्र 1.36 में 2l लम्बाई की एक छड़ AB है जिस पर एकसमान रूप से वितरित कुल आवेश है। तार पर आवेश का रैखिक घनत्व λ=q2l है। हमें छड़ के समद्विभाजक पर बिन्दु O से दूरी r पर स्थित किसी बिन्दु P पर विद्युत् क्षेत्र की गणना करनी है।
माना छड़ पर बिन्दु O से दूरी x पर लम्बाई dx का एक अल्पांश C है। इस अल्पांश C पर आवेश =λdx. अल्पांश C के कारण बिन्दु P पर विद्युत् क्षेत्र
→dE1=14πε0λdx(r2+x2) (दिशा −−→CP में)
इसी प्रकार, बिन्दु O के दूसरी ओर दूरी x पर लम्बाई dx के अल्पांश D के कारण बिन्दु P पर विद्युत् क्षेत्र
−−→dE2=14πε0λdx(r2+x2) (दिशा −−→DP में)
स्पष्टत: −−→dE1 तथा −−→dE2 परिमाण में बराबर हैं। यदि −−→dE1 तथा −−→dE2 को क्षैतिज व ऊर्ध्वाधर अवयवों में वियोजित करें तो हम पाते हैं कि इनके ऊर्ध्वाधर अवयव परस्पर बराबर तथा विपरीत दिशा में होने के कारण निष्फल हो जाते हैं तथा क्षैतिज अवयव एक दिशा में होने के कारण जुड़ जाते हैं। अत: बिन्दु P पर परिणामी विद्युत् क्षेत्र
−→dE=∣∣∣−−→dE1∣∣∣cosθ+∣∣∣−−→dE2∣∣∣cosθ , जहाँ ∣∣∣−−→dE1∣∣∣=∣∣∣−−→dE2∣∣∣ (दिशा −−→OP में)
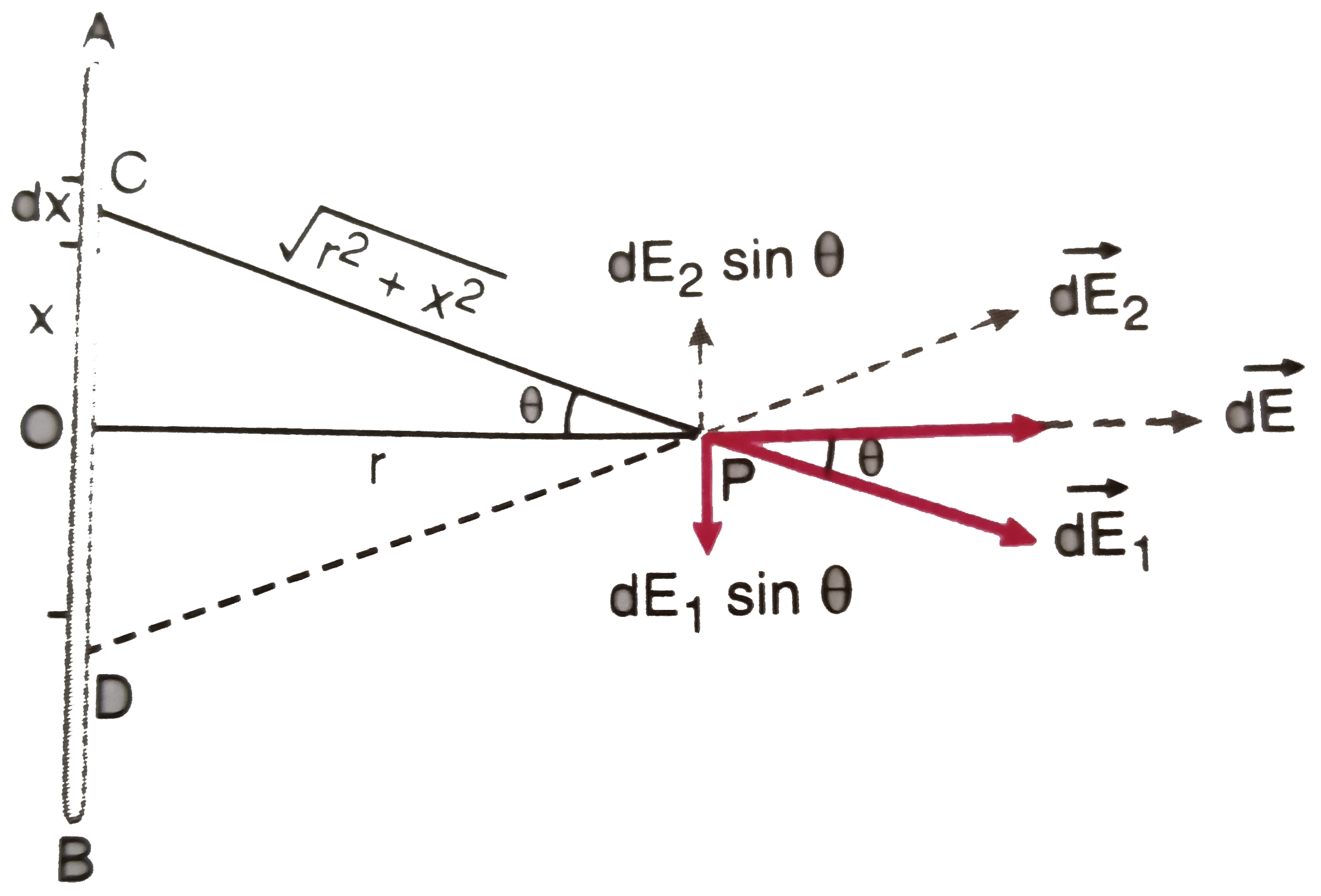
⇒−→dE=2×14πε0λdx(r2+x2)cosθ
चूँकि x/r=tanθ,∴dx=rsec2θdthη (दिशा −−→OP में)
अब यदि छड़ AB के सिरों A व B द्वारा बिन्द P पर अन्तरित कोण 2α है तो सम्पूर्ण छड़ के कारण विद्युत् क्षेत्र, उपर्युक्त समीकरण का θ=0 से ∞ तक समाकलन करके ज्ञात किया जा सकता है, अत: सम्पूर्ण छड़ के कारण बिन्दु P पर
विद्युत् क्षेत्र की तीव्रता →E=∫α0λ2πε0rcosθdθ=λ2πε0r(sinθ)α0=λsinα2πε0r
=12πε0λrl√r2+l2=14πε0qr√r2+l2 न्यूटन/कूलॉम (दिशा −−→OP में)
(क्योंकि sinα=l/√r2+l2 तथा q=λ.2l)
विशेष परिस्थिति-यदि छड़ अनन्त लम्बाई की है तो,→E=∫π/20λ2πε0rcosθdθ=λ2πε0r(sinθ)π/20=12πε0λr=14πε0qrl न्यूटन/कूलॉम (दिशा −−→OP में)|
स्पष्टत: विद्युत् क्षेत्र की तीव्रता छड़ के बिन्दु की लम्बवत् दूरी के व्युत्क्रमानुपाती है तथा छड़ से दूर उस बिन्दु को ओर दिष्ट है।
Topper's Solved these Questions
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - तथ्यात्मक प्रश्न13videos
विद्युत् आवेश तथा क्षेत्र
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - अभ्यास ( प्रत्येक प्रश्न में दिए गए विकल्पों में से सही विकल्प चुनिए )15videos
विद्युत् आवेश तथा क्षेत्र
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत-चुंबकीय तरंगे EXERCISE - वस्तुनिष्ठ प्रश्न42videos
विद्युत-चुंबकीय तरंगे
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् विभव तथा धारिता EXERCISE - इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए166videos
विद्युत् विभव तथा धारिता
Similar Questions
सू्खे बालों पर कंघी करने पर कंघी में कागज के छोटे-छोटे टुकड़ों को अपनी ओर आकर्षित करने का गुण आ जाता है, क्यों ? यदि बाल गीले हों तब क्या होगा ?
58:16View Solutionधनावेशित काँच की छड़ को अनावेशित चालक से स्पर्श कराया जाता है। छड़ की आवेश :
46:40View Solutionविद्युत-चुंबकीय तरंगों का आविष्कार किया था :
52:45View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
VP−VQ तथा VB−VA
 54:23View Solution
54:23View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ ||
08:10View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
02:52View Solutionकूलम्ब नियम पर कुछ प्रश्न || विद्युत क्षेत्र एवं विद्युत् क्षेत्र की तीव्रता || वैद्युत क्षेत्र रेखाएँ
42:49View Solutionकिसी बिन्दु-आवेश के कारण तथा आवेशों के निकाय के कारण विद्युत् क्षेत्र
01:29:51View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
01:24:31View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
40:32View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
38:22View Solutionआवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
46:59View Solutionसमरूप आवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
01:23:57View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
01:21:57View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
43:47View Solutionसीधे धारावाही चालक तार के कारण किसी बिन्दु पर चुंबकिय क्षेत्र की तीव्रता
44:38View Solution

