त्रिज्या R के एक वलय पर आवेश q एकसमान रूप से वितरित है। इसकी अक्ष पर केन्द्र से x दूरी पर स्थित बिन्दु पर विद्युत् क्षेत्र की तीव्रता ज्ञात कीजिए।
चित्र 1.37 में मीटर त्रिज्या का एकसमान वलय है जिस पर q कूलॉम आवेश एकसमान रूप से वितरित है। हमें इसकी अक्ष पर केन्द्र O से x दूरी पर स्थित किसी बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। वलय की परिधि की एकांक लम्बाई पर आवेश (अर्थात् रेखीय आवेश घनत्व)
λ=q2πr कूलॉम/मीटर
माना वलय की परिधि के बिन्दु A पर dl लम्बाई का एक छोटा अवयव है जिस पर आवेश dq=λdl होगा। इस आवेश अवयव के कारण बिन्दु P पर विद्युत् क्षेत्र की तीव्रता
−−→dE1=14πε0λdl(r2+x2) (−−→OP दिशा में)
इसी प्रकार, वलय के व्यासाभिमुखी विपरीत और बिन्दु B पर dl लम्बाई के अवयव के कारण बिन्दु P पर विद्युत क्षेत्र की तीव्रता
−−→dE2=14πε0λdl(r2+x2) (−−→BP दिशा में)
स्पष्टतः −−→dE1 तथा −−→dE2 परिमाण में बराबर है। अब यदि −−→dE1 तथा −−→dE2को क्षैतिज व ऊर्ध्वाधर अवयवों में वियोजित करें तो हम पाते हैं कि इनके ऊर्ध्वाधर अवयव परस्पर बराबर एवं विपरीत दिशा में होने के कारण एक-दूसरे को निष्फल कर देते हैं तथा क्षीतज अवयव परस्पर जुड़ जाते हैं। अत: बिन्दु P पर परिणामी विद्युत क्षेत्र की तीव्रता
−→dE=−−→dE1cosθ+−−→dE2cosθ (−−→OP दिशा में)
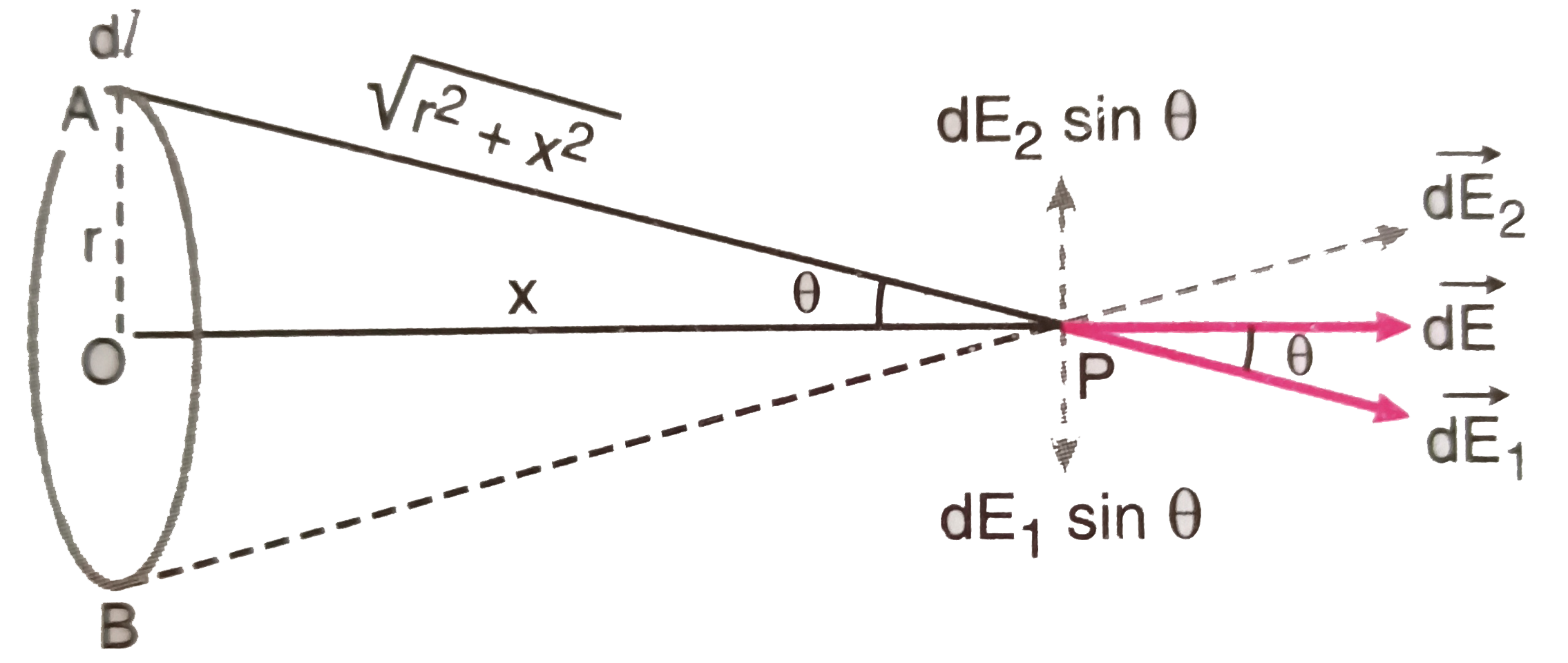
⇒−→dE=2×14πε0λdl(r2+x2)×x√r2×x2
(क्योंकि cosθ=OPAP=x√r2+x2)
=12πε0λdlx(r2+x2)3/2
अब सम्पूर्ण वलय के कारण बिन्दु P पर विद्युत् क्षेत्र की तीव्रता, वलय के ऐसे सभी छोटे-छोटे अवयवों के कारण विद्युत् क्षेत्र की तीव्रताओं के योग के बराबर होगी, अर्थात्
→E=∑12πε0λdlx(r2+x2)3/2 (−−→OP दिशा में)
=12πε0λx(r2+x2)3/2∑dl=12πε0λx(r2+x2)3/2×πr
(क्योंकि वलय की अर्द्धपरिधि के लिए ∑dl=πr)
या →E=12πε0qx(r2+x2)3/2न्यूटन/कूलॉम (∵q=λ.πr)
स्पष्टत: एकसमान धनावेशित वलय के कारण उसकी अक्ष के किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता, वलय की अक्ष के अनुदिश बाहर की ओर होगी, लेकिन यदि वलय ऋणावेशित है तो इसकी दिशा, अक्ष के अनुदिश वलय की ओर होगी।
Topper's Solved these Questions
- विद्युत् आवेश तथा क्षेत्र BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - तथ्यात्मक प्रश्न
13 Videos
- विद्युत् आवेश तथा क्षेत्र BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - अभ्यास ( प्रत्येक प्रश्न में दिए गए विकल्पों में से सही विकल्प चुनिए )
15 Videos
- विद्युत-चुंबकीय तरंगे BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत-चुंबकीय तरंगे EXERCISE - वस्तुनिष्ठ प्रश्न
42 Videos
- विद्युत् विभव तथा धारिता BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् विभव तथा धारिता EXERCISE - इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए
166 Videos
Similar Questions
सू्खे बालों पर कंघी करने पर कंघी में कागज के छोटे-छोटे टुकड़ों को अपनी ओर आकर्षित करने का गुण आ जाता है, क्यों ? यदि बाल गीले हों तब क्या होगा ?
View Solutionधनावेशित काँच की छड़ को अनावेशित चालक से स्पर्श कराया जाता है। छड़ की आवेश :
View Solutionविद्युत-चुंबकीय तरंगों का आविष्कार किया था :
View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
VP−VQ तथा VB−VA

View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
View Solutionआवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
View Solutionसमरूप आवेशित वलय के कारण उसकी अक्ष पर विद्युत क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solution
