Dry air was passed successively through a solution of 5g of a solute in 180g water and then through pure water. The loss in weight of solutionwas 250g and that of pure solvent 0.04g . The molecular weight of the solute is
31.25
3.125
312.5
None of these
The correct Answer is:A
To find the molecular weight of the solute, we can use the information provided in the problem and apply the concepts of colligative properties, specifically Raoult's law and the concept of vapor pressure lowering.
1. Understanding the Problem:
- We have a solution containing 5 g of a solute in 180 g of water.
- The loss in weight of the solution when dry air is passed through it is 250 g, and the loss in weight of pure solvent (water) is 0.04 g.
2. Identify Variables:
- Let W1 = loss of mass of the solution = 250 g
- Let W2 = loss of mass of the solvent = 0.04 g
- Let Ws = mass of solute = 5 g
- Let Ww = mass of solvent (water) = 180 g
3. Using the Formula:
- According to the formula derived from Raoult's law, we have:
ΔPP=W2W1+W2
- Here, ΔP is the change in vapor pressure, and P is the initial vapor pressure.
4. Substituting the Values:
- Substitute W1 and W2 into the equation:
ΔPP=0.04250+0.04=0.04250.04
5. Calculating the Ratio:
- Calculate the value:
ΔPP≈0.04250=0.00016
6. Using the Formula for Molar Mass:
- The molar mass of the solute can be calculated using the formula:
ΔPP=WsM⋅(Ww/Mw)
- Where M is the molar mass of the solute and Mw is the molar mass of water (approximately 18 g/mol).
7. Rearranging the Formula:
- Rearranging gives us:
M=Ws⋅MwW1+W2⋅PΔP
- Substituting the known values:
M=5⋅18250+0.04⋅250.040.04
8. Calculating Molar Mass:
- Calculate M:
M=90250.04⋅6251=31.25 g/mol
Final Answer:
The molecular weight of the solute is approximately 31.25 g/mol.
- We have a solution containing 5 g of a solute in 180 g of water.
- The loss in weight of the solution when dry air is passed through it is 250 g, and the loss in weight of pure solvent (water) is 0.04 g.
- Let W1 = loss of mass of the solution = 250 g
- Let W2 = loss of mass of the solvent = 0.04 g
- Let Ws = mass of solute = 5 g
- Let Ww = mass of solvent (water) = 180 g
- According to the formula derived from Raoult's law, we have:
ΔPP=W2W1+W2
- Here, ΔP is the change in vapor pressure, and P is the initial vapor pressure.
- Substitute W1 and W2 into the equation:
ΔPP=0.04250+0.04=0.04250.04
- Calculate the value:
ΔPP≈0.04250=0.00016
- The molar mass of the solute can be calculated using the formula:
ΔPP=WsM⋅(Ww/Mw)
- Where M is the molar mass of the solute and Mw is the molar mass of water (approximately 18 g/mol).
- Rearranging gives us:
M=Ws⋅MwW1+W2⋅PΔP
- Substituting the known values:
M=5⋅18250+0.04⋅250.040.04
- Calculate M:
M=90250.04⋅6251=31.25 g/mol
The molecular weight of the solute is approximately 31.25 g/mol.
Topper's Solved these Questions
- SOLUTIONSBOOK - A2ZCHAPTER - SOLUTIONSEXERCISE - Elevation Of Boiling Point
21 Videos
- SOLUTIONSBOOK - A2ZCHAPTER - SOLUTIONSEXERCISE - Depression Of Freezing Point
28 Videos
- SOLUTIONSBOOK - A2ZCHAPTER - SOLUTIONSEXERCISE - Raoult'S Law, Ideal And Non-Ideal Solutions, Azeotropes
37 Videos
- SOLID STATEBOOK - A2ZCHAPTER - SOLID STATEEXERCISE - Section D - Chapter End Test
30 Videos
- SURFACE CHEMISTRYBOOK - A2ZCHAPTER - SURFACE CHEMISTRYEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Dry air was successively passed through a solution of 5g solute in 80g water and then through pure water. The loss in weight of solution was 2.5g and that of pure water was 0.04g. What is mol. wt. of solute ?
View SolutionDry air was suvvessively passed through a solution of 5g solute in 80g water and then through pure water. The loss in weight of solution was 2.5g and that of pure water was 0.04g. What is mol.wt. of solute?
View Solution
Knowledge Check
Dry air was passed successively through solution of 5g of a solute in 180g of water and then through pure water. The loss in weight of solution was 2.50g and that of pure solvent 0.04g. The molecualr weight of the solute is:
A(a) 31.25B(b) 3.125C(c ) 312.5D(d) None of theseDry air was passed successively through a solution of 5 gm of a solute in 80 gm of water and then through pure ware. The loss in weight of solution was 2.50 gm and that of pure solvent 0.04 gm. What is the molecular weight of the solute
A70.31B7.143C714.3D80Dry air was passed successively through a solution of 5 g of a solutte in 80 g of water and then through pure water. The loss in mass of solution was 2.5 g and that of pure solvent was 0.04 g The molecular mass of the solute is :
A70.31B3.125C312.5Dnone of these
Dry air was passed through a solution containing 20g of a substance in 100-0g of water and then through pure water. The loss in mass of the solution was 2.945g and that of pure water was 0.059g. Calculate the molar mass of the substance.
View SolutionDry air was passed successively through a solution of 5g of a solute in 180g of water and then through pure water and then through pure water. The loss in weight of solution was 2.5g and that of pure solvent 0.04g. The molecular weight of the solute is:
View SolutionDry air is passed through a solution containing 10 g of the solute in 90 g of water and then through pure water. The loss in weight of solution is 2.5 g and that of pure solvent is 0.05 g. Calculate the molecular weight of the solute.
View SolutionLowering of vapour pressure is determined by Ostward and Walner dynamic method. It is based on the principle, when air is allowed to pass through a solvent or solution, it takes up solvent vapour with it to get itself saturated with vapours at that temperature.
dry ari → solution PA−−→solventAP+A−−→Anhy.CaCl2→ air.
A and B are weighted separately before and after passing dry air. Loss in weight of each set, gives the lowering of vapour pressure. The temperature of air, the solution and the solvent is kept constant.
Dry air was passed through 5 g of solute iini 80 g of water and then through pure water. The loss in weight of solution was 2.5 g and that of pure water was 0.04 g. The molecule weight of solute is:
View SolutionLowering in vapour pressure is determined by Ostwald and Walker dynamic methed. It is based on the prinicipal , that when air is allowed to pass through a solvent or solution, it takes up solventvapour with it to get itself saturated at that temperature
I and II are weighted separately before and after passing dry air. Loss in mass of each set, gives the lowing of vapour pressure. The temperature of air, the solution and the solvent is kept constant.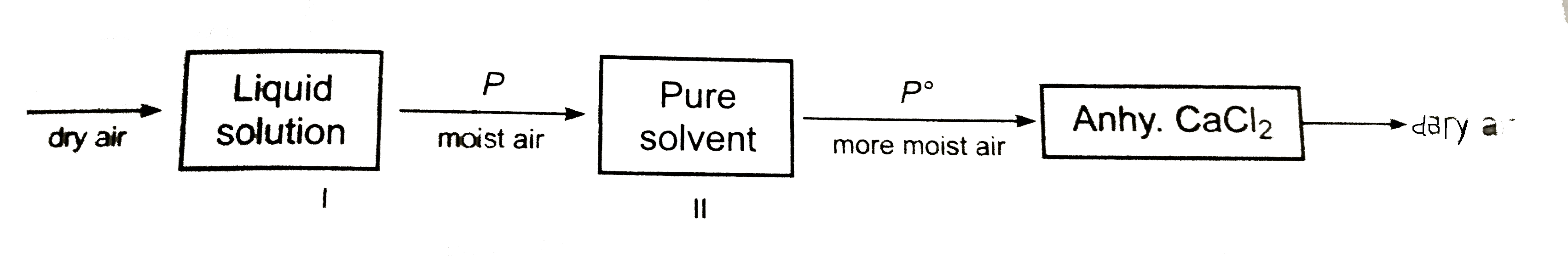
Dry air was passed thorough 9.24 g of solute in 108 g of water and then through pure water. The loss in mass of solution was 3.2 g and that of pure water 0.08 g . The molecular mass (g/mol) of solute is nearly :
View Solution
