The length of the unit cell edge of a lattice metal is 350 pm .Thus volume of atoms in one mole of the metal is

A

$9.21 c m^{3}$

B

$7.25 c m^{3}$

C

$1.21 c m^{3}$

D

$4.00 c m^{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

In a bcc struture , the atoms lough each other along the body diagonaql.

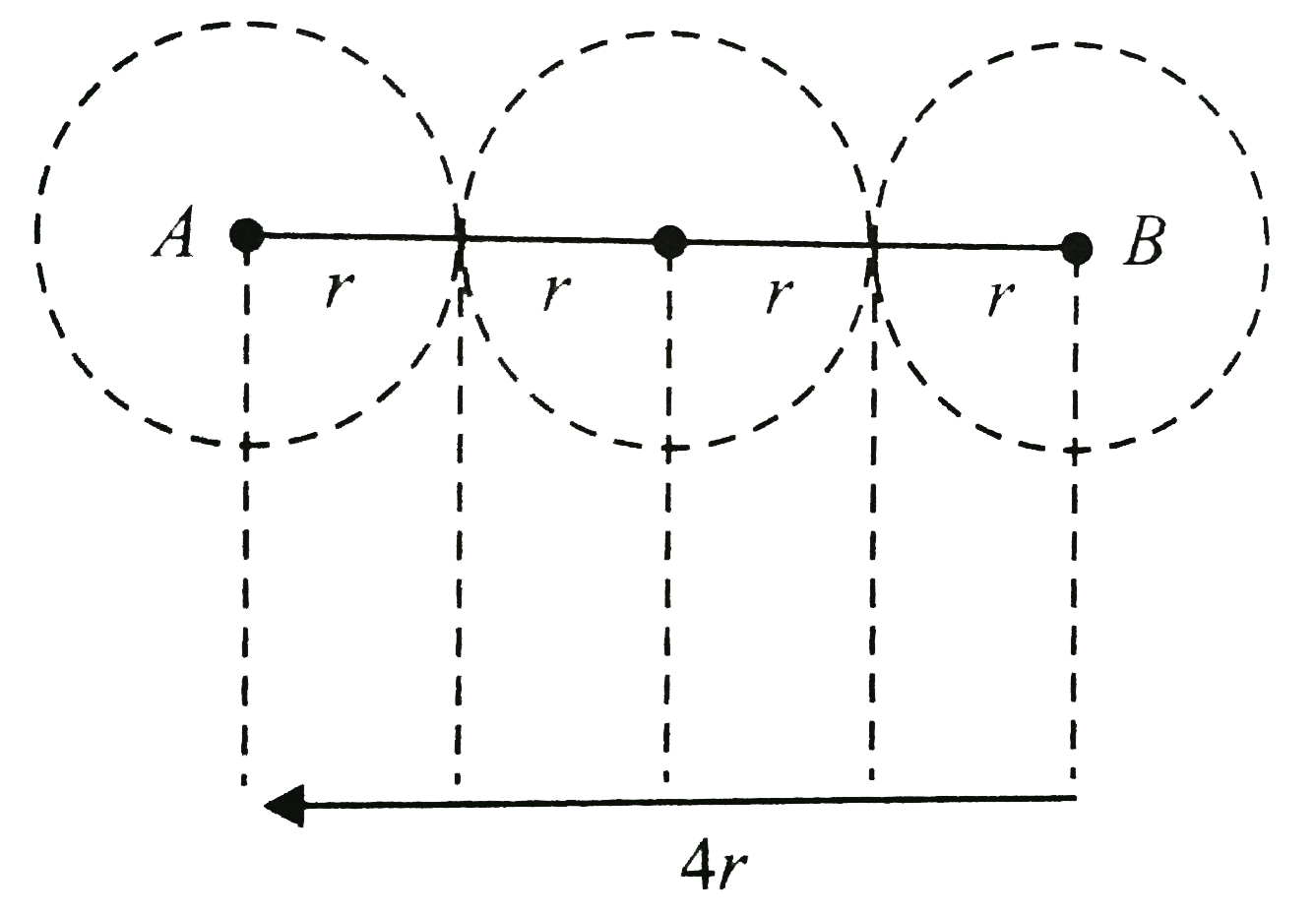
Radius of the atom $= r$
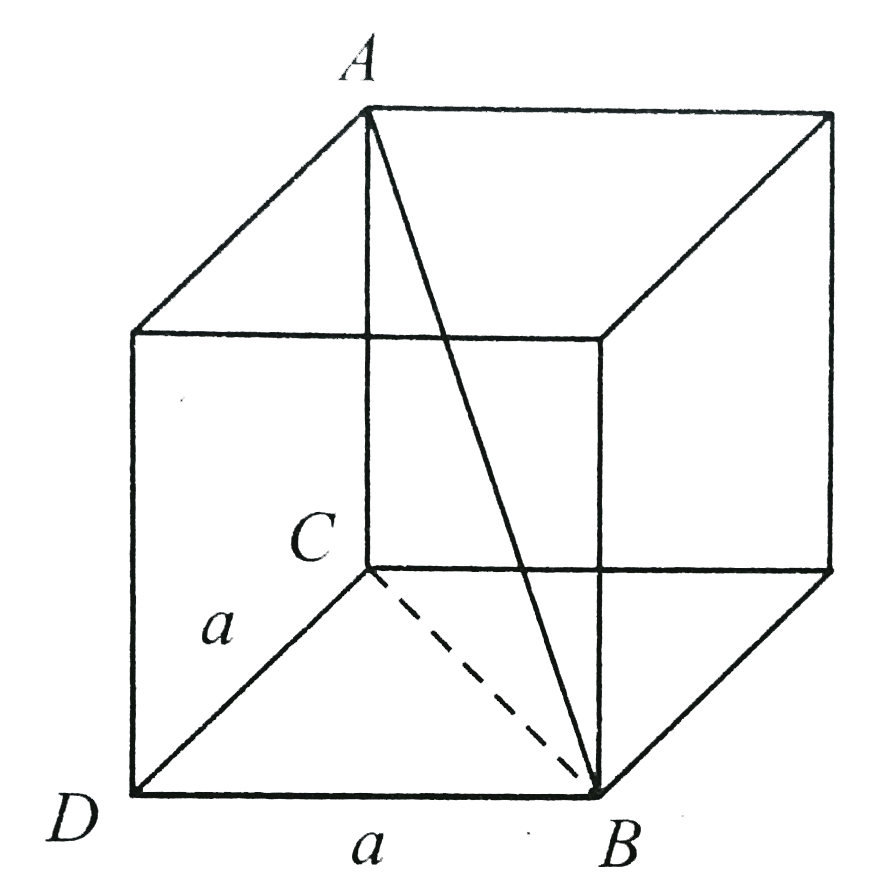
$A B^{2} = B C^{2} + A C^{2}$
$B C^{2} = B D^{2} + C D^{2} = a^{2} + a^{2} = 2 a^{2}$
$A B^{2} = 2 a^{2} = 2 a^{2} + a^{2} = 3 a^{2}$
$A B = \sqrt{3 a}$

But $A B = 4 r$
$4 r = \sqrt{2 a} \Rightarrow r = \sqrt{2 a} / 4$
$r = \sqrt{3} \times \frac{350}{4}$ pm
$= \sqrt{3} \times \frac{350}{4} \times 10^{- 12} m$
$= \sqrt{3} \times \frac{350}{4} \times 10^{- 19} c m$
$= 154.14 \times 10^{- 19} c m$
Volume of one atoms $\frac{4}{2} π r^{3} = \frac{4}{3} π {(154.14 \times 10^{- 19})}^{3} c m^{3}$
$= 1.53 \times 10^{- 23} c m^{3}$
volume of $N_{0}$ atoms is one mole of the metal
$= 6.02 \times 10^{23} \times 153 \times 10^{- 23} c m^{3}$
$= 9.21 c m^{3}$

|

Updated on:21/07/2023

Class 12 CHEMISTRY THE SOLID STATE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A metallic element crystallizes in simple cubic lattice. Each edge length of the unit cell is 3 Å.The density of the element is $8 g / c c$ . Number of unit cells in 108 g of metal is
A $1.33 \times 10^{20}$
B $2.7 \times 10^{22}$
C $5 \times 10^{23}$
D $2 \times 10^{24}$
Question 2 - Select One
A metallic element has a cubic lattice. Each edge of the unit cell is 2Å. The density of the metal is 2.5 g $c m^{- 3}$ .The unit cells in 200g of the metal are
A $1 \times 10^{25}$
B $1 \times 10^{24}$
C $1 \times 10^{22}$
D $1 \times 10^{20}$
Question 3 - Select One
A metallic element has a cubic lattice. Each edge of the unit cell is 2 Å. The density of the metal is $25 g c m^{- 3}$ . The number of unit cells in 200 g of the metal will be:
A $1 \times 10^{25}$
B $1 \times 10^{24}$
C $1 \times 10^{22}$
D $1 \times 10^{20}$

A2Z-SOLID STATE-Ssc, Fcc, Bcc, Nearest Neighbouring Distance, Next-Nearest Neighbouring Distance, Packing Fraction

Home
Ask Doubt
Profile